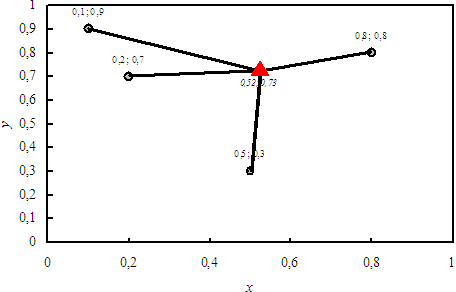
Finds the optimal location, with
coordinates X, Y, of a facility, P (red triangle
in the Figure) —the source—, so as to minimize
z, total cost of transportation to all the given
destinations (4 points in the Figure), these requiring
given quantities of goods, the capacities, Q, at given unit
costs, C. (Direction of flow is immaterial.)
The coordinates of P (X and Y)
are assumed continuous. (An alternate, discrete strategy would be
to give a set of candidate locations to optimize from.)
Point P is found by a minimization method.
A graph of the source coordinates and minimum cost
—X, Y and z*—
is made versus Q1 varying from 0 % to 100 %
(of ∑iQi).
Remark that the final result must obviously be z = 0,
and, for an RP (see '¹', below), (X, Y) = (1, 0). |
 |
¹ If n < 0,
the destinations are the |n| vertices of a generated
regular polygon (RP) inscribed in a unit circle, counterclockwise,
with first point (+1, 0).
² (Suggested values.) The "circuity factor"
is the quotient 'real distance' ⁄ 'straight line distance'.
Examples
n = −5 (1 1 1 1 1) → (3.078 1 1 1 1);
[Francis & White,
1974]: (p 189) n = 4, Q = (1, 1, 1, 1), C ≡ 1,
Coords = (0,0, 0,10, 5,0, 12,6) → P = (4, 2);
(p 205, Pr. 4.29-a) n = 3, Q = (1, 3, 1),
C ≡ 1, Coords = (0,0, 2,0, 0,2) → P = (2, 0),
see the graph.
[Love et al.,
1988]: (p 17, Exa. 2.2) n = 4, Q = (1, 2, 2, 4),
C ≡ 1, Coords = (1,1, 1,4, 2,2, 4,5) → P ≅
(2.6, 3.8), z = 195.76 (× 9⁄100 = 17.618)
NB: if using Internet Explorer, some symbols may not show
(such as "approximately equal"). |