©
Optimal facility location (continuous)
Finds the optimal location of a facility, the source, for minimum total cost of transportation to given destinations.
2025.Feb.19 21:11:17
n (2 ≤ |n| ≤ 20) No. of destinations, < 0 for RP, regular polygon¹. •
Context:  Case 1 -- pentagon Lisboa/Setúbal/Évora/Santarém/Leiria
Q [item] Capacities, Qi or "weights" (demand of each destination, usually per year: item, kg, m³, etc.). •
C [$ ⁄ km-item] Unit transportation cost, ignored² (made ≡ 1) for RP. (If circuity factor³, use, e.g., 1.3–1.6.) •
Coords [km] Points' coordinates, given as (xi, yi), i = 1..n ignored² (calculated) for RP. •
Distance norm 1   2 (Euclidean) 3   4   ∞ Distance norm (or "measure").
itmax, tol, monit Iterations (max.), tolerance for (final) cost, monitoring (for iterative minimization). •
Show values Shows the coordinates of the graph.
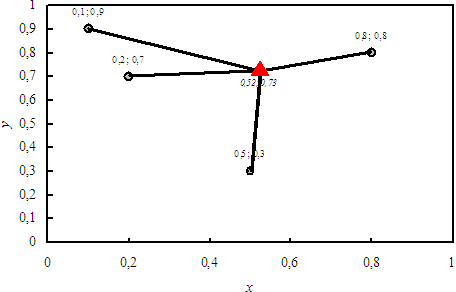
  Finds the optimal location, with coordinates X, Y, of a facility, P (red triangle in the Figure), for a source so as to minimize z, total cost of transportation to all the given destinations (4 points in the Figure), these requiring given quantities of goods, the capacities, Q, at given unit costs, C. (Direction of flow is immaterial.)
  The coordinates of P (X and Y) are assumed continuous. (An alternate, discrete strategy would be to give a set of candidate locations to optimize from.) Point P is found by a minimization method.
  A graph of the source coordinates and minimum cost —X, Y and z*— is made versus Q1 varying from 0 % to 100 % (of ∑iQi). For a regular polygon, remark that the final result must obviously be (X, Y) = (1, 0) and z = 0.		 optiloc

¹ For n < 0, the destinations are the |n| vertices of a generated regular polygon (RP) inscribed in a unit circle, with first point (+1, 0), and costs made unity.

² Although ignored, the correct number of (any) values must be supplied !

³ The "circuity factor" is the quotient 'real distance' ⁄ 'straight line distance' (suggested value).

References: Plate: FaciLoc

• Buescu, J., 2009, O mistério do armazém absorvido.Pdf*, Ingenium (in Portuguese, "The mystery of the absorbed warehouse").

• Hutt, Michael F., Programming, Nelder-Mead Simplex Fortran 90.

• Dennis, Jr., J. E., and Robert B. Schnabel, 1996, "Numerical methods for unconstrained optimization and nonlinear equations", SIAM, Philadelphia, PA (USA). . ISBN 0-89871-364-1 (pp 168–174.pdf).

• Burden, Richard L. and J. Douglas Faires, 1997, 6.th. (2004, 8.th) ed., "Numerical analysis", Brooks/Cole Publishing Company, Pacific Grove, CA (USA). ISBN 0-534-95532-0 (pp 607 ff.).

• Biegler, L. T. (research group): nonlinear equations.pdf (=) AdvProcSysEng.ing (Carnegie Mellon Univ.).

• Ortega, J. M. and W. C. Rheinboldt, 1970, "Iterative solutions of nonlinear equations in several solutions", Academic Press, London (UK). ISBN 0-12-528550-7 (pp 189–200: secant methods.pdf).

• Walton, Andrew G.: Solution of nonlinear algebraic equations.pdf (=), Imperial College London.

• Mathews, John H., 1987, "Numerical methods for computer science, engineering, and mathematics", Prentice-Hall, Inc., Englewood Cliffs, NJ (USA). ISBN 0-13-626656-8. Broyden's method.

*"Pdf" means a scanned (image) 'pdf'.

• 1867-11-03: Kutta, Martin Wilhelm († 1944-12-25, 77 yrs.).

 
 
Valid HTML 4.01! IST http://web.tecnico.ulisboa.pt/~mcasquilho/compute/com/Fx-2optiloc.php
Created: 2008-11-03 — Last modified: 2021-07-22