Wiki**3

Bottom-up parsers start from the input tokens and try to build increasingly complex structures until the initial symbol is reached.

The bottom-up parsers covered in this section are the ones belonging to the LR family (left-right rightmost derivation). These parsers are also known as shift/reduce parsers, after the actions they perform (shift = input consumption; reduce = node building). The parsers covered are LR(0) (a simple parser without any kind of lookahead), SLR (a parser that builds only when the input matches the elements in the follow set of a rule being reduced), and LALR(1) (a parser that restricts the follow symbols that can be matched in each state).

The sections below describe, first, the LR(0) and SLR(1) algorithms, and then, the LALR(1) algorithm. All three parsers share the same "shift" and "goto" entries, but differ in the restrictions put on "reduce" actions.

If the parse table contains conflicts, the grammar is said not to belong to that class, e.g., a grammar is said to be SLR(1) if its SLR(1) parse table does not contain any conflicts.

Building SLR Parse Tables

For building SLR tables we will define the notion of LR(0) item.

An LR(0) item is, informally, a production with a dot (•). The dot represents the portion of the rule that was seen by the parser so far. When the dot crosses over a symbol (advancing its position within the rule), the parser has performed a shift action (if the symbol is a terminal) or a reduce (if the symbol is a non-terminal).

For instance:

 E -> • A B C
 E -> A • B C

Internally, the parser may use a pair of integers for representing an item (one for the rule, another for the dot's position).

For each production in a grammar, there is a set of LR(0) items, each corresponding to a possible position of the dot.

The main idea is to build an automaton that recognizes viable prefixes from the input. This automaton may be thought of as an NFA in which every single LR(0) item and corresponding transition is considered. This NFA could then be converted into a DFA and minimized. This process is, however, too long and, since a direct approach exists, unnecessary.

The following steps describe the direct construction of the DFA.

The first step is to build the augmented grammar. This is a grammar like the original, but with an additional rule S' (S is the start symbol):

 S' -> S $

This rule indicates that when S (the start symbol) is reduced, then the input should be accepted, i.e., we would go from item S'->•S$ to item S'->S•$.

Like for lexical analyzers, we will define two primitive functions: ε-closure and goto (similar to "move"), that will allow us to describe an algorithm for building the DFA.

ε-closure

Consider I a set of LR(0) items. The following conditions apply to rules in ε-closure(I):

1. Initially, all elements of I are in ε-closure(I)
2. If A->α•Bβ is in ε-closure(I) and B->γ is a production, the add B->•γ to ε-closure(I)

(repeat until the ε-closure(I) is unchanged)

Example:

Consider the following grammar (rule 0 corresponds to the augmented grammar):

0) E' -> E $
1) E  -> E + T
2) E  -> T
3) T  -> T * F
4) T  -> F
5) F  -> ( E )
6) F  -> id

Then:

 I = {[E'->•E$]}
 ε-closure(I) = {[E'->•E$], [E->•E+T], [E->•T], [T->•T*F], [T->•F], [F->•(E)], [F->•id]}

Goto

The goto function is formally defined as goto(I,X) (I is a set of LR(0) items, and X is a grammar symbol).

 goto(I,X) = ε-closure({[A->αX•β]: ∀[A->α•Xβ]∈I})

Informally, if γ was a viable prefix for the elements of I, then γX is a viable prefix for the elements of goto(I,X).

Example:

 I = {[E'->E•$], [E->E•+T]}
 goto(I,+) = ε-closure({[E->E+•T]}) = {[E->E+•T], [T->•T*F], [T->•F], [F->•(E)], [F->•id]}

Building the DFA

The DFA (a set of sets) starts by containing a single element, consisting of the set obtained by computing the ε-closure of the singular set {[S'->•S$]} (S is the start symbol):

 DFA = { ε-closure({[S'->•S$]}) }

Then, repeat until it is not possible to add any further elements: for each element (set) I in the DFA and for each grammar symbol X, add goto(I,X) (if not empty) to the DFA.

Example:

Considering the grammar above, the initial configuration is:

 DFA = {I0} = {ε-closure({[E'->•E$]})}

With:

 I0 = E'->•E$
      E ->•E+T
      E ->•T
      T ->•T*F
      T ->•F
      F ->•(E)
      F ->•id

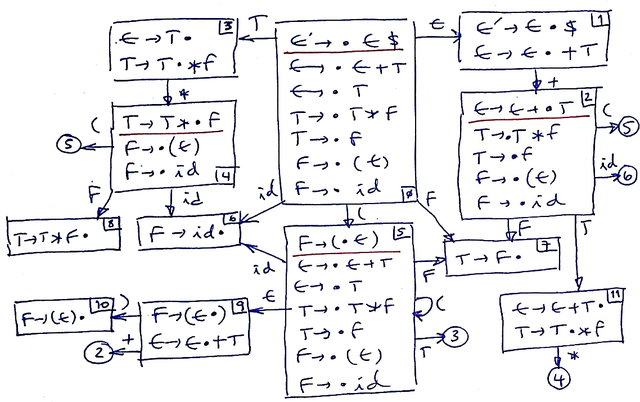
Then, applying the goto function as described above (essentially, we will look only to the symbols immediately in front of the dot), we get the following sets in the DFA (its states):

 I0 = E'->•E$    I1 = E'->E•$    I5 = F->(•E)   I6 = F->id•    I4 = T->T*•F   I11 = E->E+T•
      E ->•E+T        E ->E•+T        E->•E+T                       F->•(E)         T->T•*F
      E ->•T                          E->•T     I2 = E->E+•T        F->•id
      T ->•T*F   I3 = E ->T•          T->•T*F        T->•T*F                   I8 = T->T*F•
      T ->•F          T ->T•*F        T->•F          T->•F     I9 = F->(E•)
      F ->•(E)                        F->•(E)        F->•(E)        E->E•+T   I10 = F->(E)•
      F ->•id    I7 = T ->F•          F->•id         F->•id

Graphically:

The items above the red line correspond to kernels, i.e., the items that, in each state, characterize the state, since they are not derivable from any other items in the same state.

State 1 is the accepting state.

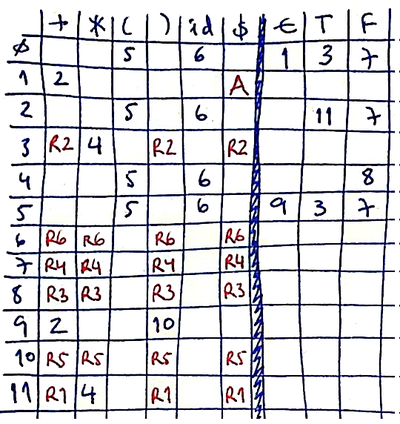
The Parse Table

The SLR(1) parse table is built, as mentioned above, based on the transitions of the DFA and on the FOLLOWs associated with reduced non-terminals (in each state where reductions occur -- the dot is at the end of the LR(0) item, meaning that all of its components have been either seen or reduced and they are available on the parser's stack).

The parse table has two zones, that associate states and symbols: action (shifts, reduces, accept), defined over states and terminal symbols (as well as with the end of phrase); and goto (defined over states and non-terminal symbols; associated with transitions after reducing non-terminals).

Assuming that the DFA has been built and, thus, the I₀ ... I_n states are known, the following steps produce the parse table:

1. State i is corresponds to I_i; the corresponding actions are:
   • If [A->α•aβ] (a is a terminal) is in I_i and goto(I_i,a) = I_j, then define action[i,a] = shift j
   • If [A->α•] is in I_i, then define action[i,a] = reduce A->α for all α ∈ FOLLOW(A) (A≠S', S' being the start symbol)
   • If [S'->S•$] (S' being the start symbol) is in I_i, then define action[i,$] = ACCEPT
2. For state i and A a non-terminal symbol, define goto(i,A) = j if goto(I_i, A) = I_j

All cells left empty correspond to syntax errors.

If step 1 above produces cells with multiple values, i.e., a shift and a reduce or more than one reduce, then the parse table has action conflicts and the grammar is said not to be SLR(1). A grammar is said to be SLR(1) if an SLR(1) parser can be built, that is, if there are no conflicts in the parse table.

Considering our example grammar, the following parse table would result from applying the steps above:

Exercises: SLR(1)

• Bottom-Up Parsing/SLR(1) Exercise 01
• Bottom-Up Parsing/SLR(1) Exercise 02
• Bottom-Up Parsing/SLR(1) Exercise 03

Exercises: LALR(1)

• LALR(1) Example 1
• Example 2: SLR(1)
• Example 3: SLR(1)
• Example 4: LALR(1)
• Example 5: LALR(1) - appeared in Test 2, 2012/06/06
• Example 6: LALR(1) - appeared in Test 2, 2015/06/19
• Example 7: LALR(1) - appeared in Test 2, 2015/06/19
• Exercise 8: LALR(1) - S -> G b b etc.
• Exercise 9: LALR(1) - E -> [ E ; L ] etc.
• Exercise 10: LALR(1) - S -> i S etc.
• Exercise 11: LALR(1) - A -> B y y etc.
• Exercise 12: LALR(1) - A -> B x y etc.
• Exercise 13: LALR(1) - A -> A B A x etc.