Difference between revisions of "Theoretical Aspects of Lexical Analysis/Exercise 4"
From Wiki**3
< Theoretical Aspects of Lexical Analysis
| Line 1: | Line 1: | ||
{{TOCright}} | {{TOCright}} | ||
| − | ==Problem | + | ==Problem == |
Use Thompson's algorithm to build the NFA for the following regular expression. Build the corresponding DFA and minimize it. | Use Thompson's algorithm to build the NFA for the following regular expression. Build the corresponding DFA and minimize it. | ||
| Line 212: | Line 212: | ||
{{CollapsedCode|Minimization tree| | {{CollapsedCode|Minimization tree| | ||
| − | [[image:aula3p4mintree.jpg| | + | [[image:aula3p4mintree.jpg|350px]] |
}} | }} | ||
| − | The tree expansion for non-splitting sets has been omitted for simplicity ("a" transition for non-final states and the {0, 2} "a" and "b" transitions. The final states are all indistinguishable, regarding both "a" or "b" transitions (remember that, at this stage, we assume that individual states -- i.e., the final states -- are all indistinguishable). | + | <!--The tree expansion for non-splitting sets has been omitted for simplicity ("a" transition for non-final states and the {0, 2} "a" and "b" transitions. The final states are all indistinguishable, regarding both "a" or "b" transitions (remember that, at this stage, we assume that individual states -- i.e., the final states -- are all indistinguishable). |
| − | + | --> | |
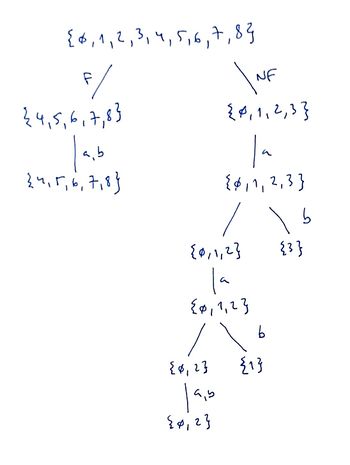
Given the minimization tree above, the final minimal DFA is as follows: | Given the minimization tree above, the final minimal DFA is as follows: | ||
Revision as of 09:53, 24 June 2016
Contents |
Problem
Use Thompson's algorithm to build the NFA for the following regular expression. Build the corresponding DFA and minimize it.
- (a|b)*abb(a|b)*
Solution
The non-deterministic finite automaton (NFA), built by applying Thompson's algorithm to the regular expression (a|b)*abb(a|b)* is the following:
| NFA |
|---|
|
|
Applying the determination algorithm to the above NFA, the following determination table is obtained:
| Determination table |
|---|
|
{ |
Graphically, the DFA is represented as follows:
| DFA |
|---|
|
|
The minimization tree is as follows:
| Minimization tree |
|---|
Given the minimization tree above, the final minimal DFA is as follows:
| Minimal DFA |
|---|
|
|