Simulates the height, h,
of a liquid with random volume, V, with a Gaussian distribution
of given parameters μ and σ.
The sphere is a storage tank with small openings at the top and bottom.
If the volume of liquid exceeds the capacity of the sphere,
there will be spill, the frequency of which should be minimized.
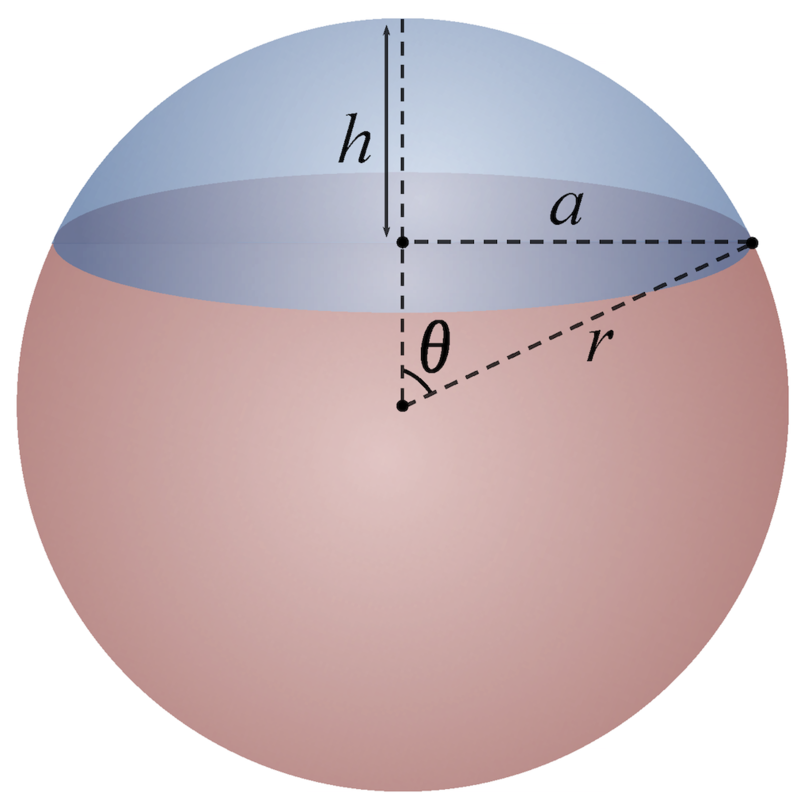
The volume of the liquid as a function of height
is given by V =
(1⁄3) π h² (3R − h),
going from V = 0 for h = 0 (empty) to
V = (4⁄3) π R³
for h = 2R (full). (In the figure*, h
increases downwards, but here it is assumed upwards.)
For the simulation, h
has to be calculated from V, leading to the (analytic) solution
of a cubic
(case 7, derivation .pdf .xlsx).
Plots the density (f) and cumulative distribution
(F) for the simulated variable. |
 |



