Software Specification: Introduction to Dafny

Software Specification, MEIC @ IST, 2020/21

João F. Ferreira

Dafny

• Programming language designed for reasoning
• Language features drawn from:
  • Imperative programming: if, while, :=, class, ...
  • Functional programming: function, datatype, codatatype, ...
  • Proof authoring: Lemma, calc, refines, inductive predicate, ...

Dafny is aimed at reasoning

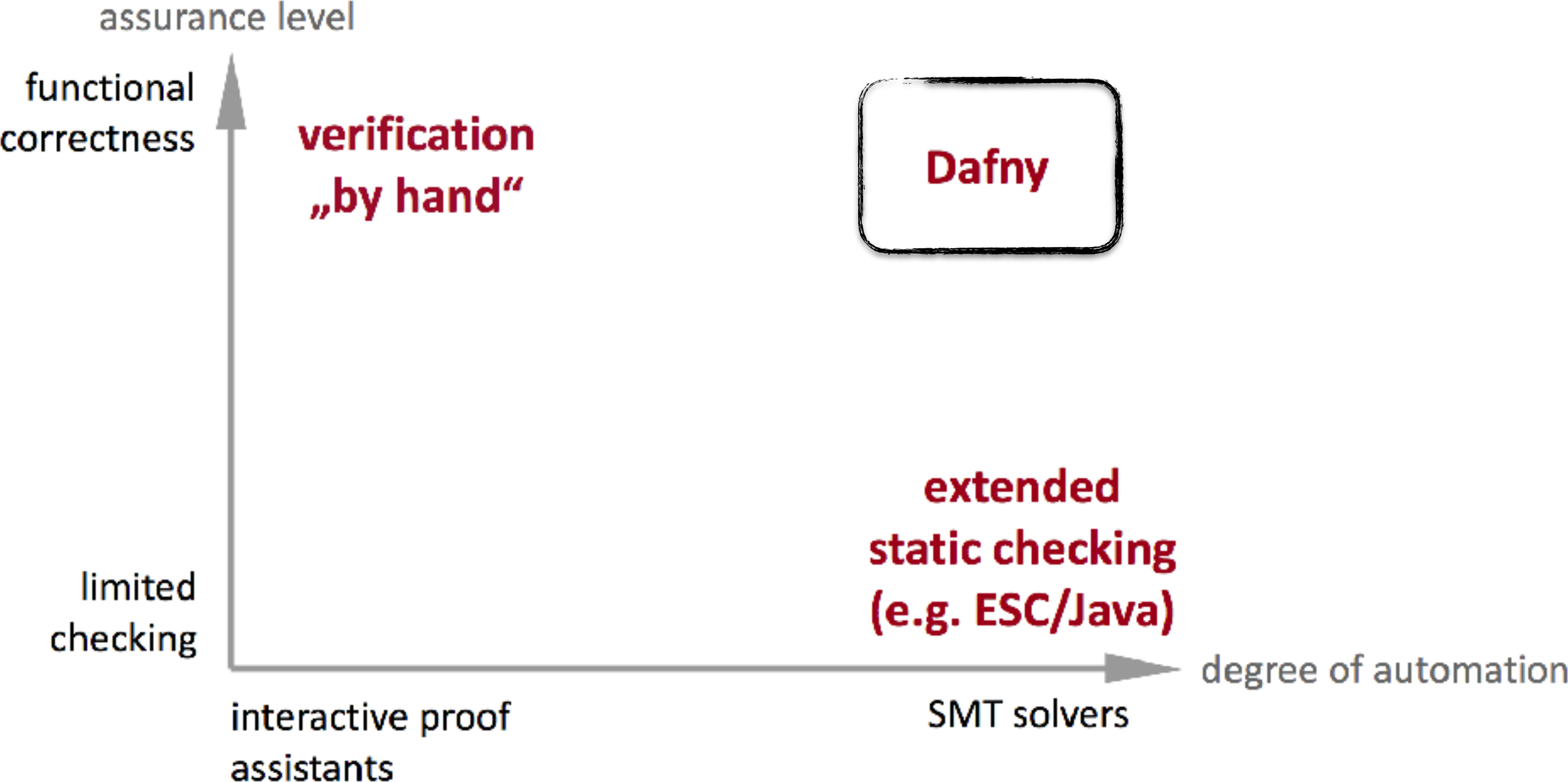
Dafny's Architecture

• Dafny uses Boogie as an intermediate verification language
• The generation of verification conditions occurs at the Boogie level
• The generated conditions are then checked by an external solver / theorem prover

Methods and Contracts

• Methods compute one or more values and may change state.
• Methods declared outside classes are allowed

method between (p: int, r: int) returns (q: int)
 requires r-p > 1
 ensures p < q < r
{
 q := (p+r) / 2;
}

Preconditions and Postconditions

method MultipleReturns(x: int, y: int) 
                   returns (more: int, less: int)
 ensures less < x
 ensures x < more
{
    more := x + y;
    less := x - y;
}

Does this program meet the specification?

Try it online: https://rise4fun.com/Dafny

Preconditions and Postconditions

method MultipleReturns(x: int, y: int) 
                   returns (more: int, less: int)
 requires 0 < y
 ensures less < x
 ensures x < more
{
    more := x + y;
    less := x - y;
}

• Add pre-condition: we need to assume that $0\lt y$
• In general, there are two main causes for Dafny verification errors:
  • specifications that are inconsistent with the code
  • situations where it is not "clever" enough to prove the required properties.

Local Variables

• Local variables are declared with the var keyword, and can optionally have type declarations:
  • var x:int;
• Unlike method parameters, where types are required, Dafny can infer the types of local variables in almost all situations
  • var x := 0;
• Multiple variables can be declared at once:
  • var x:int, y:nat;
• The type of each variable must be given individually
  • This fails:    var x, y : int;

Exercise: Encode the following example in Dafny and read the error messages.

method m1() {
    var a := 0;
    a := 1;
    var a := 2;
    var b:int;
    var c;
    var d:int, e:bool := 0;
    var f, g := 0, false;
    var h, i:int;
}

Methods: Opacity

method Triple(x: int) returns (r: int)
 ensures r == 3*x
{
    var y := Double(x);
    r := y + x;
}

method Double(x:int) returns (r:int)
 ensures r == 2*x

This follows our discussion on Design by Contract.

Try it online: https://rise4fun.com/Dafny

Methods: Opacity

• Dafny "forgets" about the body of every method except the one it is currently working on.
• This helps us reason about our programs: we can analyze each method in isolation (given the annotations for the other methods).
• We don't care at all what happens inside each method when we call it, as long as it satisfies its annotations.
• This works because Dafny will prove that all the methods satisfy their annotations, and refuse to compile our code until they do.

Exercise: Write a method Max that takes two integer parameters and returns their maximum. Add appropriate annotations and make sure your code verifies.

Assertions

method Abs(x: int) returns (y: int)
 ensures 0 <= y
{
    if x < 0 {
        return -x;
    } else {
        return x;
    }
}

method TestAbs() {
    var v := Abs(3);
    assert 0 <= v;
}

Assertions can be introduced at any point. An assertion says that a particular expression always holds when control reaches that part of the code.

Assumptions

method Abs(x: int) returns (y: int)
 ensures 0 <= y
{
    if x < 0 {
        return -x;
    } else {
        return x;
    }
}
method TestAbs() {
    var v := Abs(3);
    assume v==3;
    assert 0 <= v;
    assert v==3;
}

Assumptions can be introduced at any point.

Functions

• Functions in Dafny define mathematical functions (no side-effects).
• Functions can be used in specifications!
• Example:

function abs(x: int): int
{
    if x < 0 then -x else x
}

method m2() 
{
    assert abs(3) == 3;
}

Functions are transparent

function abs(x: int): int
{
    if x < 0 then -x else x
}

method m2() 
{
    assert abs(3) == 3;
}

• Unlike methods, Dafny does not forget the body of a function when considering other functions. So it can expand the definition of abs in the above assertion and determine that the result is actually 3.

Exercise: Write a function max that returns the larger of two given integer parameters. Write a test method using an assert that tests your function.

Exercise: Change the specification of the method Max to use your new function.

Compiling Dafny Programs

We are not going into much detail for now, but it is possible to compile Dafny programs. Example:

method Main() 
{
    print("Hello World\n");
}

To verify, compile, and run the program:
dafny /compile:3 Main.dfy

Compiling Functions

• Functions are never part of the final compiled program: they are tools to help us verify our code.
• However, sometimes it is convenient to use a function in real code, so one can define a function method, which can be called from real code.
• Functions declared as function method are compiled and can be called from real code.

Exercise: Change your test method for Max to capture the value of max to a variable, and then do the checks from the exercise using the variable. Dafny will reject this program because you are calling max from real code. Fix this problem using a function method.

Exercise: Define the Fibonacci function and write a method with assertions that test your function.

The Fibonacci function is defined as:

Loop Invariants

• We are already familiar with the concept of loop invariant
• In Dafny, we use the keyword invariant to identify loop invariants:

method m4(n: nat)
{
    var i := 0;
    while i < n
        invariant 0 <= i
    {
        i := i+1;
    }
    assert i==n;
}

Loop Invariants

• When you specify an invariant, Dafny proves two things: the invariant holds upon entering the loop, and it is preserved by the loop
  • By preserved, we mean that assuming that the invariant holds at the beginning of the loop, we must show that executing the loop body once makes the invariant hold again.
• Dafny can only know upon analyzing the loop body what the invariants say, in addition to the loop guard (the loop condition)

Exercise: Write a method Exp that takes an integer $m$, a natural $n$, and returns $m^n$. Write the specification in terms of a separate, recursive function exp.

Exercise: Consider the following function definition:

function fib(n: nat): nat
{
   if n == 0 then 0 else
   if n == 1 then 1 else fib(n - 1) + fib(n - 2)
}

Turning this function into a function method would be extremely slow, as this version of calculating the Fibonacci numbers has exponential complexity.

Write a verified iterative algorithm that computes the $n^{th}$ Fibonacci number.

Credits

• These slides use the framework reveal.js and were produced using vim and Ubuntu.
• Some slides and examples are based on material available online by Michael J. C. Gordon and Rustan Leino. Some material is taken from Dafny's tutorial.