For my first post I’ll take a theorem from algebra whose proof I didn’t like. I’ll show the proof I came up with. I don’t know if it coincides with the proof in the book in the book I’ve been reading (Altman and Kleiman) because their proof looks like symbol salad. I mean, look at this.
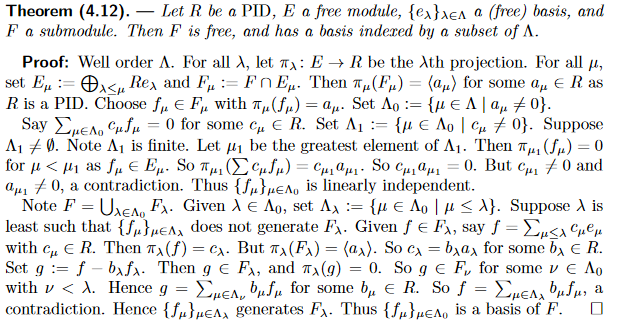
To their credit, it is a very compact proof. Maybe I’ll look at it in a few months and think “what a neat proof”, but today is not that day, so I will write down my long, possibly overcomplicated proof, in hopes that 1) it is right and 2) it helps someone else understand what’s going on here.
So what will we be doing here? We will prove the theorem that states that, given a free module $M$ over a nice enough ring, any submodule $N \subseteq M$ is also free, with rank (“dimension”) less than or equal to the rank of $M$. If you don’t understand what these words mean, you are probably not the target audience for this post. Sorry.
Visualizing Modules and The Case for $\Z^2$
I find it useful to have a “prototype module” in mind that I can visualize, in order to get an idea of the phenomena that can happen and to guide me in constructing proofs. We do this all the time in linear algebra: we make drawings of planes and vectors orthogonal to planes and lines and so on. However, general modules are trickier to visualize. Nevertheless, in my experience, $\Z^2$ as a module over $\Z$ is a nice example.
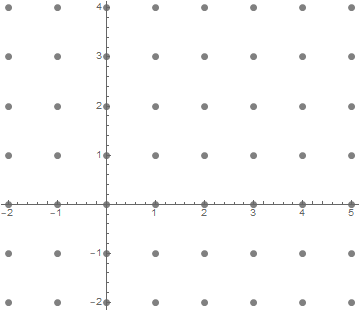
It is an easy module to visualize, but, as we will see, displays a nice range of pathologies.
For our first part, we will categorize the submodules of $\Z^2$. There is more than one way to do this, but we will try to do it as algebraically as possible, in order to make an argument that can be generalized to other modules. By analogy with our study of linear algebra, we predict that there are only three kinds of submodules: the null submodule, one-dimensional submodules, and two-dimensional submodules. Here, we already see the first example of something that doesn’t happen in linear algebra: a submodule can be two-dimensional without being the whole.
So, let’s see how we could construct a basis for some arbitrary submodule of $\Z^2$. In linear algebra, the strategy goes as follows (for finite dimension, at least). Let $N$ be a submodule (subspace) of $M$.
- Is $N$ the null subspace? If so, the empty set is a basis of $N$. Otherwise, let $v_1 \in N \setminus \{0\}$.
- Is $N$ spanned by $v_1$? If so, the set $\{v_1\}$ is a basis of $N$. Otherwise, let $v_2 \in N \setminus \langle v_1 \rangle$.
- Is $N$ spanned by $\{v_1, v_2\}$? If so, this set is a basis of $N$. Otherwise, let $v_3 \in N \setminus \langle v_1, v_2 \rangle$.
And so on…
Problem: this argument does not transfer over to general modules, because it relies on the statement that if $v$ is not in the span of some linearly independent set $A$ then $A \cup \{v\}$ is linearly independent. Unfortunately, this is not true outside of a field. For example, set $A = \{(3,0)\}$ and $v = (2,0)$ in $\Z^2$. Therefore, the previous algorithm fails. Is there a way to fix it, at least for the case of $\Z^2$?
If we’re trying to find a basis for a (non-null) submodule $N$ of $\Z^2$, we could start by picking a random nonzero element $n \in N$. However, we could have the bad luck of picking a “too complex” element. For example, even if $N$ were the $x$ axis, we could have randomly chosen $n = (6,0)$, and then we’re out of luck because even though this vector does not span $N$ it is also linearly dependent from all other elements. In order for this process to have a chance to work out, we need to find a way to “minimize” a vector.
In this particular case, the problem is that $n$ is a multiple of 6. If we set $\hat n = n/6$, we would indeed have a basis for $N$. There are more complicated cases where dividing by the biggest number we can isn’t enough, however. For example, if $N’ = 3\Z \times 0$ dividing by 6 will give us a vector that is not in N’, and so cannot be a basis for it. Nevertheless, even in this case, there exists a biggest number by which you can divide without leaving $N’$, namely $2$, and $n/2$ does form a basis for $N’$.
Therefore, something we might look into is finding ways to “simplify” randomly picked vectors, so that we have a chance at creating a base with them. In our example, the problem was that the vector was a multiple of some number, so we might expect that it would be a good idea to divide by the greatest common multiple of all the coordinates. This is the first indication we have that it might be good to restrict our attention to principal ideal domains: a PID is, morally speaking, a ring where we can take greatest common divisors.
So, returning to our general context, let $M$ be a free module. In other words, we can assume without loss of generality that it is of the form $R^{\oplus \Lambda}$ for some index set $\Lambda$. Given $m \in M$, define $\hat m$ as $m/g$, where $g$ is the GCD of the coordinates of $m$. This makes sense because, in the example of $\Z^2$, we’re making $m$ as small as possible. More rigorously, consider the ideal generated by the coordinates of $m$. Since $R$ is a PID, this ideal is generated by some $g \in R$, and every coordinate in $m$ is of the form $m_\lambda = g \hat m_\lambda$. Define $\hat m$ as the vector whose coordinates are the $\hat m_\lambda$. Note that the $\hat m_\lambda$ are coprime, which corresponds to them being minimal in some sense.
Note that this isn’t exactly well-defined, because there are multiple values of $g$ that qualify as “the GCD of the $m_\lambda$”. However, it is well-defined up to product by units. Furthermore, it apparently relies on the particular representation of $M$ as a sum of $R$s. However, this is (somewhat surprisingly) not the case, because it is (up to product by unit) the only element of $M$ with this property: $m$ is a multiple of $\hat m$, and if $m$ is a multiple of some $m’$ then $m’$ is a multiple of $\hat m$.
These “minimal vectors” (i.e. vectors whose coordinates are all coprime) can be used to generate “lines”. In good old linear algebra, given any vector $v$, we could visualize the span of $v$ as an unbroken line, but this intuition fails for modules. Taking the hat operation makes this intuition work again: the span of $\hat v$ can be seen as an unbroken line in the direction of $v$, while the span of $v$ might be “incomplete” and riddled with holes. However, note that this might be undesired: our submodule $N$ itself might have holes in the direction of $v$, in that $\hat v$ might not be in $N$, so we still have to find a minimal vector in $N$ itself.
Let’s go back to our algorithm to find a basis of a linear subspace of a vector space:
- Is $N$ the null subspace? If so, the empty set is a basis of $N$. Otherwise, let $v_1 \in N \setminus \{0\}$.
- Is $N$ spanned by $v_1$? If so, the set $\{v_1\}$ is a basis of $N$. Otherwise, let $v_2 \in N \setminus \langle v_1 \rangle$.
- Is $N$ spanned by $\{v_1, v_2\}$? If so, this set is a basis of $N$. Otherwise, let $v_3 \in N \setminus \langle v_1, v_2 \rangle$.
And so on…
Let us try to modify this algorithm in order to make it work for general modules. First, as we’ve already seen, we probably don’t want the vectors $v_1, v_2, \dots$ themselves, but rather some divisor of them. As such, given $v \in N$, $v \neq 0$, define $\tilde v$ as the smallest multiple of $\hat v$ that lies in $N$. Intuitively, this corresponds to “following along the direction of $v$ and stopping as soon as we find an element of $N$”. Of course, we do need to show that such a smallest multiple of $\hat v$ exists, but there we are once again saved by the fact that $R$ is a PID. Indeed, consider the set $B$ of scalars such that $b \hat v \in N$. It is obvious that $B$ is an ideal, which means it has some generator $b_0$. Then, simply define $\tilde v$ as $b_0 \hat v$. This might be starting to get confusing, so here is a diagram exemplifying what all these symbols mean.
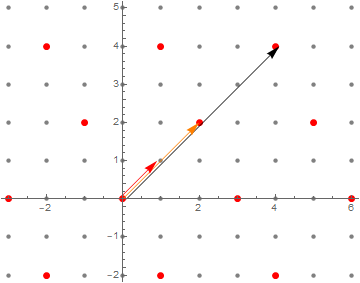
Back to our algorithm, let us try the following (simple) modification:
- Is $N$ the null subspace? If so, return the empty set. Otherwise, let $v_1 \in N \setminus \{0\}$.
- Is $N$ spanned by $\tilde v_1$? If so, return the set $\{\tilde v_1\}$. Otherwise, let $\tilde v_2 \in N \setminus \langle \tilde v_1 \rangle$.
- Is $N$ spanned by $\{\tilde v_1, \tilde v_2\}$? If so, return this set. Otherwise, let $\tilde v_3 \in N \setminus \langle \tilde v_1, \tilde v_2 \rangle$.
And so on…
All we’ve changed was, upon choosing a vector, work with its tilde. Unfortunately, this only fixes step one. The two first steps are correct. In other words, if we terminate in step 1. or 2. we are guaranteed to have a basis of $N$. However, the process can fail as soon as step 3, as the following example shows.
Let $N$ be $2\Z \times 2\Z$. Suppose that, in applying the above algorithm, we begin by choosing $v_1 = (2,0)$. Then, $\tilde v_1 = v_1$. This does not span the whole set, so suppose that in choosing $v_2$ we pick $v_2 = (6,4)$. This is also its own tilde, but $\{v_1, v_2\}$ does not span $N$; for example, with them you can’t make any vector with $y = 2$.
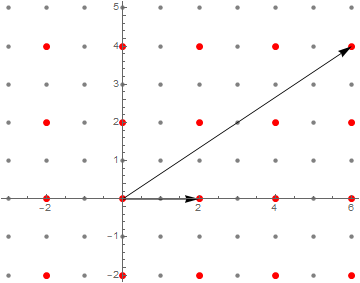
A possible objection to this example is that $v_2$ isn’t really minimal. If we look at it in isolation, sure, it is, but we do have access to $v_1$. Adding and subtracting multiples of $v_1$ to $v_2$ don’t change the span of $\{v_1, v_2\}$, so, for example, having $v_1$ and $v_2$ is just as good as having $v_1$ and $w = v_2 – 3 v_1 = (0,4)$, and note now that $w \neq \tilde w$! Indeed, $v_1$ and $w$ do span $N$, which shows that the problem with our $v_2$ was that, even though it was in fact minimal in its own line, we could disturb it using $v_1$ in order to make it non-minimal. This suggests a revision to our algorithm, and a strengthening of the concept of “tilde”.
Consider a set $A \subseteq N$. We will say $v$ is tilde-minimal in $N$ if $v = \tilde v$ (modulo product by unit). We will say $v$ is minimal with respect to $A$ if, for every $a \in A$, $v+a$ is tilde-minimal. What we have been doing is ensure that at every step the vectors we add to the list were tilde-minimal. Now that we have concluded that this is not enough, let us try to ensure that they are minimal with respect to the rest of the vectors we already have. We already have a process to construct the tilde-minimization of a vector. Can we find a way to construct an $A$-minimization of a vector, in some sense?
The obvious procedure goes as follows. Suppose $A$ and $v$ are fixed. If $v$ is $A$-minimal, we are done. Otherwise, there exists $a \in A$ such that $v + a$ is not tilde-minimal. Consider $w = v+a$, and restart the algorithm with $\tilde w$.
It is obvious by construction that, if this algorithm terminates, the result is $A$-minimal, and note that the original vector is in the span of $A \cup \{w\}$, where $w$ is the output. However, it is not clear that the process can be guaranteed to terminate. Even in $\Z^2$, it might take more than one step for it to terminate. For example, let $N$ still be $2\Z \times 2\Z$, $A = \{(2,0)\}$ and start the algorithm with $v = (2,8)$. Then, the first step of the algorithm might go as: $w = v+(2,0) = (4,8)$, $\tilde w = (2,4)$, which is still not $A$-minimal. One more step, say with $\tilde w + (2,0) = (4,4) \rightarrow (2,2)$ does result in a minimal vector, but it is obvious that this example can be adapted to make examples that take arbitrarily long to terminate.
It is tempting to use classical infinite-descent arguments to show that the algorithm halts in a finite number of steps, at least in the example of $\Z^2$, but care must be taken. For example, there is no guarantee that the norm of a vector is always decreasing. For example, still using $N = 2\Z \times 2\Z$ and $A = \{(2,0)\}$, suppose we begin the algorithm with $v = (2,4)$, and follow with $w = v + 99 \times (2,0)$. Then, as should be obvious even without doing the computations, the norm of $\tilde w$ is far greater than the norm of $v$!
However, despite this difficulty, in our particular example there is one regularity to be found: if $A$ is of the form $\{(x,0)\}$, then we know for sure that the $y$ component of the vector on which we’re doing the algorithm is constantly decreasing (in absolute value, at least), which allow us to show that the algorithm terminates. This raises the question: would it be possible to, upon choosing an element $v_1 \in N$, change basis so that $\hat v_1$ is equal to $(1,0)$? The answer is yes, though I don’t know how to generalize it to dimension higher than two.
The crucial lemma goes as follows: let $(a_1,a_2) \in \Z^2$ such that $a_1$ and $a_2$ are coprime. Then, it is possible to find a vector $(c_1, c_2)$ such that these two form a basis.
To understand why, let us first recall that $a_1, a_2$ coprime is equivalent to the existence of $b_1, b_2$ with $a_1 b_1 + a_2 b_2 = 1$. Then, we might attempt to build $(c_1, c_2)$ “by hand”. Note that we want for there to be $A, B, C, D$ such that the following things happen:
\begin{gather*}
A (a_1, a_2) + B (c_1, c_2) = (1,0)\\
C (a_1, a_2) + D (c_1, c_2) = (0,1).
\end{gather*}
Note that two of the (actually four) equations we have here look suspiciously like something we already know. For example, we want to ensure $A a_1 + B c_1 = 1$. It would be very convenient if $c_1 = b_2$ or $c_1 = a_2$, so that this equation has a known answer. It takes a bit of trial and error, but after a few iterations of applying this kind of heuristic thinking you easily reach the conclusion that $(c_1, c_2) = (b_2, -b_1)$ does in fact work, and we do indeed have a basis where one of the vectors is $(a_1, a_2)$. Don’t forget to show that the two vectors are linearly independent, and try to find a way to do it that does not rely on the fact that our ring is $\Z$.
With this in mind, we are now ready to categorize the submodules of $\Z^2$. Let $N$ be such a submodule. If $N$ is null, it is the free module generated by the empty set. Otherwise, pick $v_1 \in N$. If $\tilde v_1$ spans $N$, then it forms a basis of $N$. Otherwise, we need to apply the things we’ve done so far.
Consider a change of basis where $\hat v_1 = (1,0)$, so that $\tilde v_1$ is of the form $(x_1,0)$. Let $v_2 \in N \setminus \langle \tilde v_1 \rangle$. Note that $v_2$ is of the form $(x_2, y_2)$ with $y_2 \neq 0$, for if it were in the span of $\hat v_1$ it would also be in the span of $\tilde v_1$. (Should I prove this or is it obvious?) Now, we can apply the algorithm of $A$-minimization, described above, with $A = \{\tilde v_1\}$ and $v = v_2$. We can show that the algorithm will terminate because at each step $y_2$ gets smaller in absolute value. Note that this is the only step we’ve done so far that relies on our ring being $\Z$: we will soon describe a way to get around this.
So, now we have $\tilde v_1 \in N$ and some vector $w$ which is $\tilde v_1$-minimal. Can we show that these two vectors form a basis for $N$? Linear independence is obvious, as $w$ has non-null $y$ coordinate, so now we need only show that they generate $N$.
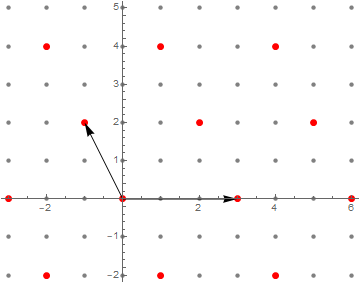
By inspecting the above image, some structure starts to appear. Since we set $\tilde v_1$ to be horizontal, it seems $N$ organizes itself as “horizontal layers”, and it makes sense (and would be necessary if this algorithm is intended to work) that $w$ would lie on the first possible layer. In other words, we claim that if $w = (x_2, y_2)$ then $y_2$ is minimal in $N$, i.e. given any $z = (x_3, y_3) \in N$ we intend to show that $y_3$ is a multiple of $y_2$. Once that is done, we know that to write $z = A \tilde v_1 + B w$ we would necessarily have $B = y_3/y_2$, and $A$ would then be completely determined by the $x$ coordinate, which gives us a path to complete the proof.
Suppose $y_3$ was not a multiple of $y_2$, and we will try to reach a contradiction. We can, without loss of generality, suppose that $y_2$ is a multiple of $y_3$, because if $g$ is the GCD of $y_2$ and $y_3$ we can write $g = C y_2 + D y_3$, and now we can work with $C w + D z$ instead of $z$. That said, we will use the fact that we have a $z$ with “smaller $y$ coordinate than $w$” to show that $w$ can’t be $\tilde v_1$-minimal after all. We will show $w$ could in fact be reduced to $z$.
Consider $\frac{y_2}{y_3} z$. It has the same $y$ coordinate as $w$, so that $w – \frac{y_2}{y_3} z$ is in the $x$ axis. It is therefore a multiple of $\tilde v_1$, let us say $K \tilde v_1$. Then, we get $w – \frac{y_2}{y_3} z = K \tilde v_1$, and we conclude that $w$ was not $\tilde v_1$-reduced after all, because $w – K \tilde v_1$ is not tilde-reduced. Thus, we reach a contradiction, and it turns out the $y$ coordinate of $w$ was minimal after all.
The proof is easy from now on, because we can easily show that $\tilde v_1$ and $w$ span $N$. Indeed, given $z = (x_3, y_3)$, we want to write it as $A \tilde v_1 + \frac{y_3}{y_2} w = z$, which is certainly possible because $z – \frac{y_3}{y_2}w$ is in the $x$ axis and also in $N$ and thus of the form $A \tilde v_1$. The proof is complete: we have shown that any submodule $N$ of $\Z^2$ is generated by zero, one or two vectors.
We are now only a tiny hop away from showing the general statement for rank two modules over a PID, because only one of the steps we did relied on our use of $\Z$: namely, when we showed that the algorithm for $A$-minimization halts by the method of infinite descent. Yet again, the fact that we are in a PID shows its usefulness, because principal ideal domains do have their own method of infinite descent in the form of the Ascending Chain Condition. Simply put, any infinite sequence $r_1, r_2, r_3, \dots$ where each $r_n$ is a divisor of the previous will eventually stabilize up to product by unit. In our particular case, we can consider the sequence of the $y_n$: since at each step the $y$ was being divided by some non-unit element (and it didn’t change when adding a multiple of $\tilde v_1$) the sequence of the $y_n$ gives us a sequence where each element is a (proper) divisor of the previous, and by the ACC it must eventually halt. Thus, we reach the conclusion:
Theorem: If $M$ is a rank two free module over a PID, any submodule $N$ of $M$ is also a free module, with rank 0, 1 or 2.
Note that the argument by ACC is effectively an argument by infinite descent, with the minor change that it uses the “divisibility partial order” instead of some order based on absolute value.
$A$-complexity
It took me a while to figure this part out, but as it turns out, the $A$-minimization algorithm above can be shown to work in finite dimension, though I haven’t yet figured out the infinite-dimensional case.
Like we did in the 2D case, the idea is to use the ACC as a monovariant. Assign each vector an element of $R$ and show that at each iteration the scalar assigned to the output is a (proper) divisor of the scalar assigned to the input. The ACC will then guarantee that the algorithm cannot go on forever.
Recall the algorithm of $A$-minimization: given $v \in M$ and $A \subseteq M$, if $v$ is $A$-minimal, we are done. Otherwise, there exists $a \in A$ such that $v + a$ is not tilde-minimal. Consider $w = v+a$, and restart the algorithm with $\tilde w$.
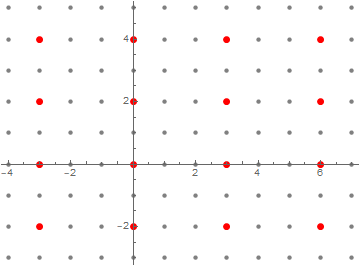
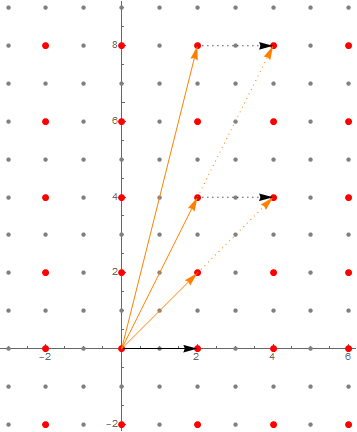
What number could we possibly assign to a vector to get this to work? It would have to be a measure of how far away our vector is from the set $A$, so it makes sense to demand that the scalar assigned to a vector $v \in M$ would be the same as the one assigned to $v+a$ for $a \in A$. Therefore, let’s look at a picture where we have drawn the sets of the form $v+A = \{\,v + a \mid a \in A\,\}$.
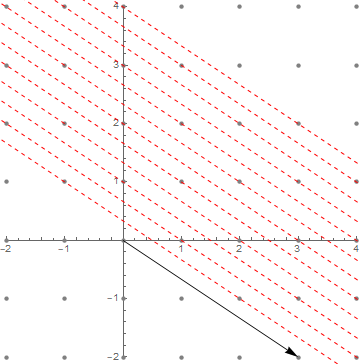
As you can see in the figure, the sets $v+A$ organize themselves as lines parallel to $A$ (as is to be expected). It would be nice to find a way to find a way to number them as $1, 2, 3, \dots$ and so on.
Now, I don’t have a very satisfactory way to explain how I got to this idea, but I hope it makes sense. We are, in a sense, trying to measure how “complex” the vectors in a line are. So far, we’ve already found a measure of how complex a vector is: the GCD of its coordinates. So what happens if we look for how complex the vectors in each of these lines are? Let’s plot the same picture, but with GCDs of coordinates annotated.
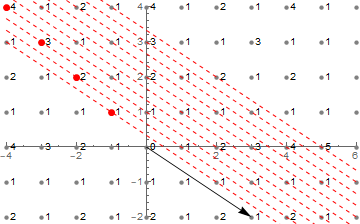
Do you see it? There are a few overlapping patterns, in fact.
- On each line, we have highlighted a point, whose “complexity value” is exactly the number we want to assign to that line,
- On each line, the highlighted point appears to have the highest complexity value in the line, and
- These points seem to be conspicuously aligned.
Let’s focus on the first two points. This seems to be in line with the idea we want: we wish to measure how complex a line is, so we find the most complex point in the line. In other words, we define
\[k_A(x,y) = \max_{(a_1, a_2) \in A} \gcd(x+a_1, y+a_2).\]
Note: this function is being applied to points, not to lines. The idea is that, since we’ll be measuring complexities of vectors anyway (to show our $A$-minimization algorithm halts), we define a function on a vector $(x,y)$, which returns the complexity of the line $(x,y)+A$.
There are two problems with this definition. First of all, how do we know such a maximum exists? And second, how do we generalize this to non-integer contexts? We’ll answer the first question shortly. As for how this generalizes to non-integer contexts, we simply apply an idea we’ve already used to generalize from integers to general PIDs: simply use a different order. Instead of thinking of the integers (or the elements of a ring) ordered by magnitude, we order them (modulo units) by divisibility. In other words, the maximum is replaced by the least common multiple. Now, let us investigate what happens in the 2D case. For simplicity, let us use an example like in the picture, where $A$ is generated by a vector $\hat a = (a_1, a_2)$, with $a_1$ and $a_2$ coprime. In this case, the expression we are maximizing when calculating $k_A(x,y)$ is given by
\[\gcd(x+ k a_1, y + k a_2), k \in \Z.\]
Now let’s apply some number theory tricks. First of all, let $b_1, b_2 \in \Z$ be such that $b_1 a_1 + b_2 a_2 = 1$. Second, we know that the GCD stays the same if we add multiples of one term to another. That is, $\gcd(A, B) = \gcd(A, B+n A)$ for any $n$. Furthermore, the GCD of two numbers is the same as the GCD of those two numbers, and zero, that is, $\gcd(A,B) = \gcd(A,B,0)$. Therefore, we can shuffle some things around to get rid of the $k$ in as many terms as possible:
\begin{align*}
\gcd(x+ k a_1, y + k a_2) &= \gcd(x+k a_1, y+k a_2, 0)\\
&= \gcd(x+k a_1, y+k a_2, b_1 (x+k a_1) + b_2(y+k a_2))\\
&= \gcd(x+k a_1, y+k a_2, b_1 x + b_2y + k)\\
&= \gcd(x+k a_1 – a_1(b_1 x + b_2y + k), y+k a_2 – a_2(b_1 x + b_2y + k), b_1 x + b_2y + k)\\
&= \gcd(x – a_1(b_1 x + b_2 y), y – a_2 (b_1 x + b_2 y), b_1 x + b_2 y + k).
\end{align*}
(In simple words, what happened here: we added an argument of the form $\text{const.} + k$ to the GCD and then removed appropriate multiples of it to the other arguments so that only the last argument depends on $k$.)
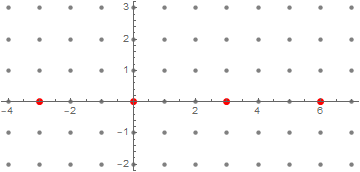
Now, if we are taking the maximum as $k$ varies over the integers, we might as well pick $k = -(b_2 y + b_1 x)$, to attain the maximum $\gcd(x – a_1(b_1 x + b_2 y), y – a_2 (b_1 x + b_2 y))$. (Check that it is actually the maximum, at least in the divisibility order!) Note that this explains the phenomenon wherein we found those red points in a line: it is actually the line given by points of the form
\[(x,y) + k (a_1, a_2) = (x,y) – (b_2 y + b_1 x)(a_1, a_2) = \dots = (a_2 x – a_1 y) (b_2, -b_1),\]
which form a line in the direction of $(b_2, -b_1)$. In our case, $(a_1, a_2) = (3,-2)$, and it is easy to check that (a possible pair) $(b_1, b_2) = (1,1)$, which results in a line with the direction of $(1,-1)$, which does match with the red points.
Motivated by how well the 2D case worked, we will now generalize the notion of $A$-complexity to the finite dimensional case.
The Finite Rank Case
Let $M$ be a finite rank module, say $R^N$. Consider a subset $A$ generated by $\hat a^1, \dots \hat a^k$, where each of these vectors has coprime coordinates $(\hat a^j_1, \dots, \hat a^j_N)$. In what follows, we will always assume $A$ is of this form. We will define the $A$-complexity of a vector $v \in M$ as
\[k_A(v) = \max_{a \in A} \gcd(v_i + a_i),\]
where the maximum is taken in the divisibility order (and is only defined modulo unit) and inside the GCD the index $i$ is implicitly varying as $i = 1, \dots, N$. What we will now show is that this is a well-defined expression, and, when applying the $A$-minimization algorithm, is guaranteed to decrease with every iteration, which shows that the algorithm halts.
First, rewrite the quantification over $a \in A$ as one over multiples of the $\hat a^j$:
\[k_A(v) = \max_{r_1, \dots, r_k \in R} \gcd(v_i + r_1 \hat a^1_i + \dots + r_k \hat a^k_i).\]
Now we can apply the previous tricks to get rid of variables. For example, suppose $b_1, \dots, b_N$ are such that $\sum b_i \hat a^k_i = 1$. Then, if $u_i = v_i + r_1 \hat a^1_i + \dots + r_{k-1}\hat a^{k-1}_i$,
\begin{align*}
\gcd(v_i + r_1 \hat a^1_i + \dots + r_k \hat a^k_i) &= \gcd(u_i + r_k \hat a^k_i)\\
&= \gcd(u_i + r_k \hat a^k_i, \left(\sum_j b_j u_j\right) + r_k)\\
&= \gcd(u_i – \hat a^k_i \left(\sum_j b_j u_j\right), \left(\sum_j b_j u_j\right) + r_k).
\end{align*}
This expression depends only on $r_k$ in the last coordinate, and so can easily be maximized (in this variable) for $r_k = -\sum_j b_j u_j$, leaving us with an expression depending only on $r_1, \dots, r_{k-1}$. The process can be iterated, which would leave us with a (terrible) explicit expression for computing $k_A(v)$, which shows it is well-defined.
Now we need only show that this is a monovariant for the $A$-minimization algorithm. Recall that the algorithm goes as follows: given $v \in M$ and $A \subseteq M$, if $v$ is $A$-minimal, we are done. Otherwise, there exists $a \in A$ such that $v + a$ is not tilde-minimal. Consider $w = v+a$, and restart the algorithm with $\tilde w$.
Therefore, it will suffice to show that if $w \not \in A$ is not tilde-minimal then $k_A(\tilde w) < k_A(w)$ in the divisibility order. More specifically, given a vector $v$ and a scalar $r$ we will show that $r k_A(v) \leq k_A(r v)$, which, together with the fact that $k_A(v) = 0$ iff $v \in A$ (which we will also shows), proves that $k_A(w)$ is a proper multiple of $k_A(\tilde w)$. All of this is happening modulo product by unit. I’m going to stop saying that things are modulo unit.
There is an “easy” way to see that $k_A(r v) = r k_A(v)$ (this is stronger than we need). If you had the patience to write down the explicit expression for $k_A(v)$ you would notice it is a GCD of things that depend linearly on the $v_i$, which clearly shows that multiplying $v$ by a scalar would multiply its $A$-complexity by that scalar. However, there is a direct and easy proof of the inequality by definition. Indeed, $r k_A(v) = \max_a r \gcd(v_i + a_i) = \max_a \gcd(r v_i + r a_i)$. This is the same as taking the maximum of $\gcd(r v_i + a_i)$, where now the $a$ are varying over $r A$ instead of $A$. Therefore, $r k_A(v) \leq k_A(r v)$.
Now, to complete the proof that for $w \not \in A$, $w \neq \tilde w$ we have $k_A(\tilde w) < k_A(w)$, we need only show that $k_A(\tilde w) \neq 0$. To do so, we will show that $k_A(v) = 0$ iff $v \in A$; this is enough because if $\tilde w$ were in $A$ so would $w$.
Obviously if $v \in A$ then $k_A(v) = 0$, so let us do the other implication. Suppose, that $k_A(v) = 0$. Then there exists $a$ such that $\gcd(v_i – a_i) = 0$. But since any number divides zero, if there was a single nonzero term in the GCD then the GCD would not be zero. Therefore, we conclude $v = a \in A$.
In conclusion:
- We have defined an object we call “the $A$-complexity of a vector”, for sets $A$ generated by $\hat a^1, \dots, \hat a^k$,
- We have shown that this is a monovariant for the $A$-minimization algorithm, which shows that
- Given any vector $v \not \in A$ there exists $w$ such that $w$ is $A$-minimal, that is, $w+a$ is tilde-minimal for all $a \in A$. Furthermore, $w$ is obtained from $v$ by repeatedly adding elements of $A$ and taking tilde, which shows that $v \in \langle A, w \rangle$.
We are now ready to rewrite our algorithm for finding a basis of a submodule. Let $M$ be a free module of finite rank. Let $N$ be a submodule of $M$. (Not to be confused with the rank of $M$ above!) Consider the following algorithm to (we hope) find a basis of $N$:
- Is $N$ the null submodule? If so, return the empty set. Otherwise, let $v_1 \in N \setminus \{0\}$.
- Is $N$ spanned by $\tilde v_1$? If so, return the set $\{\tilde v_1\}$. Otherwise, let $\tilde v_2 \in N \setminus \langle \tilde v_1 \rangle$ be $\hat v_1$-minimal.
- Is $N$ spanned by $\{\tilde v_1, \tilde v_2\}$? If so, return this set. Otherwise, let $\tilde v_3 \in N \setminus \langle \tilde v_1, \tilde v_2 \rangle$ be $\langle \hat v_1, \hat v_2 \rangle$-minimal.
And so on…
The output of this algorithm (if it halts in finite time) is a maximal set $\tilde v_1, \tilde v_2, \dots, \tilde v_k$, where each vector is minimal with regard to the previous vectors. Clearly, this set spans $N$, so what is left to show is that 1. it is linearly independent and 2. it halts at most in $K = \mathrm{rk}\, M$ steps.
Let us begin with linear independence. Suppose some non-null linear combination $\sum r_i \tilde v_i$ equals zero. We wish to make use of minimality of each vector wrt to the previous, so let $k_0$ be the biggest coefficient such that $r_{k_0} \neq 0$. We conclude
\[r_{k_0} \tilde v_{k_0} = \sum_{i=1}^{k_0 – 1} -r_i \tilde v_i.\]
Now, that looks kind of weird. For this to happen, the span of $\tilde v_1, \dots, \tilde v_{k_0 – 1}$ would need to have “holes from the point of view of $N$”: vectors which are in the span but have divisors which are not. Fortunately, we are in a position to show such holes can’t happen, that is:
Proposition: Let $\tilde v_1, \tilde v_2, \dots \tilde v_k \in N$ be such that each of these vectors is minimal (in $N$) wrt the vectors before it. (In other words, a possible output of our (hopefully) base generation procedure.) Then, the span of the $\tilde v_i$ is “free of holes in $N$”, in the sense that, for all $r \in R$, $r \neq 0$ and $v \in N$ such that $r v \in \langle \tilde v_1, \dots, \tilde v_k \rangle$, we have $v \in \langle \tilde v_1, \dots, \tilde v_k \rangle$.
Proof: Since our hypothesis is inductive, it makes sense to consider a proof by induction in $k$. The base case is trivial: for $k = 0$ the span of the vectors is the null space and there is nothing to show.
Now, let us do the induction step. Suppose the statement is true for some $k$, and let us prove it for $k+1$. Let $r \in R$, $r \neq 0$, and $v \in N$ such that
\[r v = \left(\sum_{i = 1}^k r_i \tilde v_i\right) + r_{k+1} \tilde v_{k+1}.\]
The idea is to rearrange this as (the sum on the right-hand side) equals (some multiple of something in $N$). In particular, we want to write $r v – r_{k+1} \tilde v_{k+1}$ as a multiple of something in $N$, To do so, let $g$ be the GCD of $r$ and $r_{k+1}$, and so we get
\[g (\tfrac rg v – \tfrac{r_{k+1}}g \tilde v_{k+1}) = \sum_{i = 1}^k r_i \tilde v_i,\]
and so we conclude, by the induction hypothesis, that $\tfrac rg v – \tfrac{r_{k+1}}g \tilde v_{k+1}$ can be written as a linear combination of $\tilde v_1, \dots, \tilde v_k$. Now, we can use the fact that $\tfrac rg$ and $\tfrac{r_{k+1}}g$ are coprime to write, say, $A \tfrac rg + B \tfrac{r_{k+1}}g = 1$, and so we can write
\[\text{(Some combination of $\tilde v_1, \dots, \tilde v_k$)} = B\tfrac rg v – B\tfrac{r_{k+1}}g \tilde v_{k+1} = – \tilde v_{k+1} + \tfrac rg (B v + A \tilde v_{k+1}),\]
which, unless $r = g$, contradicts the minimality of $\tilde v_{k+1}$ wrt $\tilde v_1, \dots, \tilde v_k$, for we can write $\tilde v_{k+1}$ plus a combination of the other vectors as $r/g$ times a vector in $N$.
Now, we have already shown that $\tfrac rg v – \tfrac{r_{k+1}}g \tilde v_{k+1}$ can be written as a linear combination of $\tilde v_1, \dots, \tilde v_k$, and so, since $r =g$, $v$ can be written as a combination of $\tilde v_1, \dots, \tilde v_{k+1}$, which completes the induction step. QED.
This completes the proof that the vectors obtained by the algorithm “have no holes”, and consequently that they are all linearly independent. Now, the only thing left to do is to show that there are at most $K = \mathrm{rk}\, M$ distinct vectors. The classical, linear algebra way of doing this is to use the fact that on $K$-dimensional space any set of more than $K$ vectors cannot be linearly independent. This is also true on modules over general rings, but it is a mouthful to prove. I might do a post on it sometime if I feel like it. In any case, I’ll prove the case for domains, which is a very simple adaptation of linear algebra.
The idea is as follows: given a set of vectors $v_1, \dots, v_k$, we will do some kind of “Gaussian elimination”, which results in an upper diagonal $k \times K$ matrix whose rows are nontrivial linear combinations of $v_1, \dots, v_k$. If all vectors are linearly independent, then no row may be null, but this can only happen if the matrix is not taller than it is wide: in other words, $k \leq K$.
The Gaussian elimination algorithm (on a vector space, i.e. over a field!) goes as follows. Consider the matrix
\[
\begin{bmatrix}
v_{11} & v_{12} & \cdots & v_{1K}\\
v_{21} & v_{22} & \cdots & v_{2K} \\
\vdots & \vdots & \ddots & \vdots\\
v_{k1} & v_{k2} & \cdots & v_{kK}
\end{bmatrix}.
\]
Is the first column null? If so, skip to the next step. Otherwise, assume without loss of generality (by swapping lines if necessary) that $v_{11}$ is non-null. Then, since we’re in a field, $v_{11}$ is invertible, and we may add multiples of the first line to the rest in order to get a matrix of the form
\[
\begin{bmatrix}
v_{11} & v_{12} & \cdots & v_{1K}\\
0 & v_{22} – \frac{v_{21}}{v_{11}} v_{12} & \cdots & v_{2K} \frac{v_{21}}{v_{11}} v_{1K} \\
\vdots & \vdots & \ddots & \vdots\\
0 & v_{k2} – \frac{v_{k1}}{v_{11}} v_{k2} & \cdots & v_{kK} – \frac{v_{k1}}{v_{11}} v_{1K}
\end{bmatrix}.
\]
Now, apply the algorithm recursively on the submatrix composed of the indices $\{2,\dots,k\} \times \{2, \dots, K\}$ (or, if we skipped a step because the first column was null, $\{1,\dots,k\} \times \{2, \dots, K\}$). Continue until you reach an empty matrix. The resulting matrix is definitely upper-diagonal, and each line is of the form
\[\text{(The vector that was in that line)} + \text{(A linear combination of previous vectors)},\]
so if any of the lines is null then the lines of the initial matrix must necessarily be linearly dependent. And of course, if $k > K$ then this is necessarily the case, which shows (in vector spaces) that a set of more than $K$ vectors in $K$-dimensional space must be linearly dependent.
Now here comes the magic trick: even though this argument is not applicable to general modules, because there is no guarantee that a non-null scalar is invertible, it can easily be adapted to work for domains (and, in particular, PIDs): instead of subtracting, say, $\frac{v_{21}}{v_{11}} \times \text{the first line}$ to the second line, multiply instead the second line by $v_{11}$ and subtract $v_{21}$ times the first line to it. The end result is that each line is of the form
\[\text{A non-null scalar}\times\text{(The vector that was in that line)} + \text{(A linear combination of previous vectors)},]\]
and the argument for vector spaces proceeds without a hitch. Note that we use the assumption that $R$ is a domain when we claim that “$\text{A non-null scalar}$” is indeed non-null, because all we know about it is that it is a product of non-null scalars.
This concludes the proof of the theorem for finite rank spaces:
Theorem: if $M$ is a finite rank free module over a PID $R$ and $N$ is a submodule of $M$, then $N$ is also a free module over $R$, with rank at most that of $M$.
A Negative Result: Why This Doesn’t Work in Infinite Dimension
This section is the kind of thing I feel kind of silly writing, and yet I wish it was the kind of thing I wish more people did. Mathematical proofs aren’t the result of a single avenue of research, but rather the result of several failed or partially failed attempts. However, when we are presented with the one path that did work, it leaves open the question of “why did they choose this very non-obvious path and not one of the more obvious things they could have done?”. Consequently, this section is me explaining how I figured out that the path we have taken so far can never be used to do the proof in infinite dimensions. I am not happy about this.
So, let’s lay down what we’ve got so far. We have an algorithm which will, given a submodule $N$ of $M$, create successively bigger lists of elements in $N$ such that each element is in some sense minimal with relation to the previous vectors. We have shown that these vectors are all linearly independent and their span “has no holes in $N$”, that the algorithm terminates exactly when the list of vectors spans $N$, and we guaranteed that it terminates in a finite number of steps if $M$ has finite rank. Mixing these ingredients, the proof is done for finite dimension.
To generalize the proof to infinite dimension, we would probably want to use some kind of transfinite process, or, more commonly, the doesn’t-know-ordinals-person version of that, Zorn’s lemma. To do so, we would need to find some poset corresponding to “lists of vectors that could be obtained in the process of our algorithm”, use Zorn’s lemma to prove that there is a maximal such list of vectors (which corresponds to “running the algorithm very-infinitely many times until we can’t run it anymore”) and showing that a maximal list of these vectors is in fact a basis for $N$.
The obvious thing to do would be to consider the poset $P$ of lists (or bigger – there are set theoretical details you’d need to work out first, but they’re not relevant so we’re glossing over them here) of vectors of $N$ such that each vector $v$ is $A$-reduced where $A$ is the set of vectors before $v$ in the list, ordered by $L_1 \leq L_2$ iff $L_1$ is a prefix of $L_2$. Indeed, it would not be hard to adapt the arguments for the finite rank case to show that such a list $(v_1, v_2, \dots) \in P$ would be linearly independent and “have no holes”, and it would not be a big stretch to show that any chain has an upper bound (given a bunch of lists in a chain, just take “the union of the lists”) which allows us to apply Zorn to get a maximal list. In other words, we’ve just applied the algorithm we developed as many times as we could.
This is where we run into a problem, however. How do we show that such a maximal list $L = (v_1, v_2, \dots)$ forms a basis for $N$? In the finite dimensional case the argument would go as follows: if $w$ weren’t in the span of $L$, we could apply the minimization algorithm to $w$ over $A = \langle L \rangle$ in order to get a vector $w’ \in N$ which is minimal wrt to $L$. This would contradict the hypothesis that $L$ is maximal, because we could get a bigger list by appending $w’$ to the end of $L$. Unfortunately – and this is the crucial bit – the minimization algorithm only works for finite dimension.
First of all, a weaker statement: our proof that the $A$-minimization algorithm works required that we were in finite dimension. This is because we proved that it terminates based on the quantity which we called $k_A(w)$, which we showed was well-defined (and even proposed a way to find an explicit expression for it) and showed was a monovariant in the algorithm. However, if you go back and look, you’ll notice that we assumed in the proof (but curiously, not the definition) that $A$ was finitely generated. You might think that this could be recoverable and that $k_A$ would be a well-defined object, but you would unfortunately be wrong.
Recall the (basis-of-$A$ independent) definition of $k_A(v)$:
\[k_A(v) = \max_{a \in A} \gcd(v_i + a_i).\]
In order to try and break this definition, I sought out an example over, say, $\Z$, where this GCD would take arbitrarily large values. It would need to be infinite-dimensional, and the simplest possible example is $\Z^\infty$, which is a direct sum of countably many copies of $\Z$. Now, I would need to find a vector $v$ and a sequence of vectors $a^1, a^2, \dots$ such that each vector $a^n$ satisfying that, say, $v + a^n$ is a multiple of $n$. Furthermore, we will want to ensure that $v$ is not in the span of the $a^n$, because the $A$-minimization algorithm was meant to be applied to vectors $v \not \in A$.
With these constraints, after a bit of trial and error, I came up with (a slightly more complicated version of) the following example:
\begin{gather*}
v = (1,0,0,\dots),\\
a^n = (-1, \underbrace{0, \dots, 0}_{\text{$n-1$-many zeroes}}, n, 0, \dots).
\end{gather*}
With $A = \langle a^1, a^2, \dots \rangle$, the quantity $k_A(v)$ is not well-defined, because in the “maximum” we have arbitrarily large values (because $\gcd(v_i + a^n_i) = n$) but we never attain an actual maximum. Any reasonable extension of the concept (say we use a supremum instead of a maximum, which in PID terms corresponds to taking the least common multiple) we would have $k_A(v) = 0$ in this example, which completely breaks any attempt at adapting the proof that the $A$-minimization algorithm works.
It gets worse. Not only does our proof fail, the entire algorithm fails, and the whole attempted proof fails: this set $\{a^n \mid n \in \N^+\}$ has the troubling property that, even though it fails to generate the whole set (you should check this) and is linearly independent, it cannot be extended to a basis of $\Z^\infty$. By itself, this is neither too surprising nor too worrisome: we saw examples like this right at the start, where the pair $(2,0),(0,3)$ is linearly independent in $\Z^2$ but cannot be made into a basis. To solve this problem, we spent a bunch of time coming up with criteria stronger than “linearly independent” which, if satisfied, ensure our linearly independent sets can be extended to bases. This is what we did with the definition of minimal wrt $A$, in demanding that lists of vectors $(v_1, \dots, v_n)$ satisfy the property that each $v_k$ is minimal wrt $\langle \hat v_1, \dots, \hat v_k\rangle$. The example of $(a^1, a^2, \dots)$ does not satisfy this property, but once you understand why, it is easy to adapt it to one that does:
\[b^n = (-1, \underbrace{0, \dots, 0}_{\text{$n-1$-many zeroes}}, p_n, 0, \dots), \text{ where $p_n$ is the $n$-th prime}.\]
(Exercise: show that the set of $a^i$ does not satisfy the minimality property, and show that the set of $b^i$ does.)
What this example shows is that the criterion we’ve established for the finite dimensional case falls flat in the infinite case, because even though every $b^n$ is minimal wrt the span of the previous $b^i$, the set containing all of them cannot be extended to a basis. Furthermore, this shows that the property “the list $L$ can be extended to a basis of the space” is not invariant under directed unions, that is, it is possible that $L_1 \leq L_2 \leq L_3 \leq \dots$ is an increasing sequence of lists of vectors such that each list can be extended to a basis but their union $L$ cannot. This means that an argument through Zorn’s lemma must be carefully crafted, because it cannot be taken for granted that every chain has an upper bound. It is certainly not true in the poset of lists of vectors that can be extended to bases.
Another Approach: Minimizing Coordinates
After the failure of the iterative method, I decided to try something else. Furthermore, I started thinking of how to show that rank of the submodule $N$ is less than or equal to the rank of $M$, so I began thinking about coming up with a basis “one coordinate at a time”.
Another successful idea so far has been the idea of minimization of scalars. In other words, if we have a set of things that forms an ideal, we can find a smallest possible thing. Smallest in the divisibility order, that is.
Mixing those two ideas, I cobbled together the following argument. Suppose, for the sake of argument, that $M = R^3$.
Then, a generic argument of $N \subseteq M$ is of the form $(x,y,z)$. Having the radical idea of minimizing one coordinate at a time, I thought to consider the following: define $v_1$ as an element of $N$ with minimal $x$ coordinate. Then, for any $v \in N$ I can find $a \in R$ such that $a v_1$ has the same $x$ coordinate as $v$. Now, I need to fix the $y$ coordinate, so I’ll pick $v_2$ with minimal $y$ coordinate. But I need to be careful, because I don’t want to mess up the $x$ coordinate. Therefore, I’ll pick $v_2$ with minimal $y$ coordinate, among those vectors with zero $x$ coordinate. Therefore, since $v – a v_1$ has null $x$ coordinate, I can find $b \in R$ such that $v – a v_1 – b v_2$ has null $y$ coordinate, and incidentally it still has null $x$ coordinate. The pattern should be clear by now: pick $v_3$ with minimal $z$ coordinate among those with null $x$ and $y$ coordinate, and I conclude there exists $c$ such that $v – a v_1 – b v_2 = c v_3$, and since $v$ is arbitrary the set $\{v_1, v_2, v_3\}$ spans $N$.
This argument was rather handwavy, so let me make it more rigorous. Consider $M = R^n$ and $N$ a submodule of $M$. For each $i = 1, 2, \dots, n$ define $v_i$ as an element of $N$ with minimal $i$ coordinate among those vectors $w$ with $w_1 = \dots = w_{i-1} = 0$. This exists because of the following argument. Let $I$ be the set of $r \in R$ such that there exists $w \in N$ with $w_1 = \dots = w_{i-1} = 0$ and $w_i = r$. It is easy to check that $I$ is an ideal, and so it is generated by some scalar $r_0$. Then, since this scalar is in $I$, there exists a vector, which is our $v_i$, whose $i$-th coordinate is $r_0$ and whose coordinates $1$ through $i-1$ are null. Furthermore, by definition of $I$ and $r_0$, any vector with coordinates $1$ through $i-1$ null has its $i$-th coordinate a multiple of $r_0$. (I think these last few sentences are unnecessary, are they?)
Now that we’ve created our set $v_1, \dots, v_n$, it is time to check that it is a basis. Of course, this might not be true: we never even guaranteed that these vectors are non-null, and indeed in general some of them can be. As such, we will instead consider the sublist, which we will call $L$, of those $v_i$ whose $i$-th coordinate different from zero.
Let us show that $L$ spans $N$. To do so, given $n \in N$ we will construct a linear combination of elements of $L$ that equals $n$. To this effect, consider the following inductive algorithm, which defines a sequence of scalars $a_1, \dots, a_n$:
For each $i = 1, \dots, n$:
1. If $v_i \not \in L$, set $a_i = 0$.
2. Otherwise, let $w = n – a_1 v_1 – \dots – a_{i-1} v_{i-1}$. We know inductively that $w$ has its first $i-1$ coordinates equal to zero.
3. Consequently, $w_i$ is of the form $r (v_i)_i$. Set $a_i$ to equal this $r$.
It is easy to show inductively that the finishing list satisfies $n = \sum a_i v_i$, and since all the coefficients corresponding to vectors not in $L$ are null, this proves that the vectors in $L$ span $N$.
Now, the only thing left to do is to show that the vectors in $L$ are linearly independent. But that’s easy: note that each vector $v_i$ in $L$ is the first in the list to have non-null $i$-th coordinate. This shows linear independence because given a nontrivial linear combination $\sum a_i v_i$ of elements of $L$ that equals zero, the term with biggest index $i$ such that $a_i \neq 0$ is the only one to make a contribution to the $i$-th coordinate of the sum. Therefore, the $i$-th coordinate of the sum is given by $a_i (v_i)_i$, which, because we’re in a domain and $v_i \in L$, implies $a_i = 0$, contradiction. Therefore there is no nontrivial linear combination of the $v_i \in L$ that equals zero.
Therefore, using only three or four paragraphs, we have proven the case for finite dimension which took us oh so long. Woops.
Anyway, the benefit of this argument is that it can be easily extended to infinite dimensions. Not immediately, but it is doable. Let’s begin by extending it to countable rank.
Let $M = R^\infty$, i.e. a sum of countably many copies of $R$. Then, we will construct our (hopefully) basis of $N$, say, $v_1, v_2, \dots$ in a similar way, using minimality. Unfortunately, the very same strategy does not immediately work: we cannot simply pick $v_1$ with minimal first coordinate, $v_2$ with minimal second and null first coordinate, and so on, because when we apply our algorithm to write any $n \in N$ as a linear combination of them, we have no guarantee that they don’t just “run away”. For example, if $N = M$, we could have picked, say, $v_1 = (1,1,0,0,\dots)$, $v_2 = (0,1,1,0,0,\dots)$, and so on, and with these vectors we could never write $e_1 = (1,0,0,\dots)$. In finite dimension we didn’t have this problem: since you can only “go so far right”, you always had the guarantee of termination.
The fix for this is simple: just build it all backwards. Define $v_1$ as a vector with minimal first coordinate and null second, third, and so on. $v_2$ is a vector with minimal second coordinate and null third, fourth, and so on. Then, the aforementioned process does terminate, because at each step, the biggest nonzero coordinate index is always decreasing. In other words, suppose we start with a vector $n = (n_1, n_2, \dots, n_k, 0, 0 \dots)$. Then, $n_k$ is a multiple of $(v_k)_k$, let’s say $n_k = a_k (v_k)_k$. Now, consider $n’ = n – a_k v_k$. It is easy to check that it is of the form $n’ = (n’_1, n’_2, \dots, n’_{k-1}, 0, 0, \dots)$. Repeat the process with $v_{k-1}$ and so on, and after at most $k$ steps we will have written $n = \sum a_i v_i$. This shows that these $v_i$ generate $N$, and the proof for linear independence is the same as in the finite case.
This is actually the general argument, though some changes must be made to allow for uncountably many dimensions. Note that our process is kind of iterative: we need a first dimension, a second dimension, and so on. For the countable case, this is taken care of because we know there is a bijection between the dimensions and the naturals, but for the uncountable case we need to be a bit more careful. The idea is to use the Well-Ordering Theorem from set theory, which states that any set can be well-ordered. If you don’t know what that means, umm, I’ll make a post about it sometime.
If we well-order the set of indices, then we know for sure that there exists a first element, second element, and so on, and the well-order guarantees that we can only “go down so many times”. We’ll do the details shortly but the main point is that, if we well-order the set of indices and do the above procedure (minimize each coordinate while keeping the coordinates after it null) everything works out and we reach a basis.
The Final Proof
In hindsight, this proof is actually a rewritten version of the proof we gave at the start. But I hope it’s more understandable.
Let $M = R^{\oplus \Lambda}$, where $R$ is a PID, and consider a well-ordering of $\Lambda$, which we will use along the proof. Given a submodule $N \subseteq M$, we will show that $N$ has a basis indexed on a subset of $\Lambda$.
For every $\lambda \in \Lambda$, define $v_\lambda$ as an element of $N$ with $(v_\lambda)_\eta = 0$ for $\eta > \lambda$, and $(v_\lambda)_\lambda$ minimal in the divisibility order. To show that this exists, define
\[I = \{\, w_\lambda \mid w \in N \text{ such that } w_\eta = 0 \text{ for } \eta > \lambda\,\}.\]
It is trivial to check that this is an ideal of $R$. Since $R$ is a PID, it is generated by some $a_\lambda \in R$. Since, in particular, $a_\lambda \in I$, there exists some $v_\lambda$ such that $v_\lambda = a_\lambda$ and $v_\eta = 0$ for $\eta > \lambda$.
Now, let $\Lambda_0$ be the set of indices $\lambda \in \Lambda$ such that $a_\lambda \neq 0$. We claim that the set $\{v_\lambda\}_{\lambda \in \Lambda_0}$ forms a basis of $N$.
Proof that this set is linearly independent: suppose that some nontrivial linear combination $\sum a_i v_{\lambda_i}$ equals zero. We will show that all $a_i$ are null. To do so, assume without loss of generality that every $a_i$ is not zero (we can remove zeros from the sum). Let $\lambda_0 = \max \{\lambda_i\}$, which exists because this set is finite and non-empty. Then, it is easy to check that $\left(\sum a_i v_{\lambda_i} \right)_{\lambda_0} = a_i$. But this must be zero. This is a contradiction, which means that $\lambda_0$ cannot exist after all, and so our linear combination is necessarily the trivial one.
Proof sketch that this set generates $N$ (cleaner proof in next paragraph): Let $n_0 \in N$. Consider the algorithm given as follows. Supposing $n_k$ is defined and not null, let $\lambda_k$ be the biggest nonzero index in $n_k$. Then, it is easy to check that $\lambda_k \in \Lambda_0$. Let $a_k$ be such that $(n_k)_{\lambda_k} = a_k (v_{\lambda_k})_{\lambda_k}$ (exists by definition of $v_\lambda$). Then, define $n_{k+1}$ as $n_k – a_k v_{\lambda_k}$. It is trivial to check that $\lambda_{k+1}<\lambda_k$, or, in other words, the sequence of lambdas is a monovariant. If this algorithm continued indefinitely, the set $\{\lambda_k\}_{k \in \N}$ would have a minimal element (since we well-ordered $\Lambda$), which is absurd because this would correspond to some $\lambda_{k_0}$, which cannot be minimal because it is greater than $\lambda_{k_0+1}$. Therefore, the algorithm must halt in finite time, and so some $n_k$ must be null, which shows that $n_0$ can be written as $a_0 v_{\lambda_0}+ \dots + a_{k-1} v_{\lambda_{k-1}}$, as desired.
Alternative proof that this set generates $N$ (cleaner): Suppose that $N_0 = N \setminus \mathrm{span}\{v_\lambda\}_{\lambda \in \Lambda_0}$ was non-empty. Pick an element $n_0$ of $N_0$ with minimal maximum non-null index. More clearly: for each $n \in N_0$ define $\lambda_n = \max\{\lambda \mid n_\lambda \neq 0\}$ (note that this is well-defined because $n \neq 0$). Then, the set of possible values of $\lambda_n$ has a minimum, say $\lambda_{n_0}$. Now find a contradiction, because $\lambda_{n_0} \in \Lambda_0$, so we can define $n_1 = n_0 – a_0 v_{\lambda_{n_0}}$, with the obvious $a_0$. It is trivial to check that $n_1 \in N_0$ and furthermore that $\lambda_{n_1} < \lambda_{n_0}$, contradicting the minimality of $\lambda_{n_0}$.
The proof is complete.
Wow, fantastic blog layout! How long have you ever been blogging for?
you made running a blog glance easy. The overall glance of your web
site is excellent, let alone the content! You can see similar here sklep internetowy
Hi there, simply became alert to your weblog thru Google, and located that it is really informative. I am gonna watch out for brussels. I will be grateful in the event you continue this in future. Many folks might be benefited from your writing. Cheers!
What i do not understood is in fact how you’re no longer actually much more neatly-preferred than you might be now. You’re so intelligent. You realize therefore considerably in relation to this matter, made me individually imagine it from a lot of various angles. Its like women and men aren’t fascinated unless it is one thing to accomplish with Girl gaga! Your own stuffs excellent. Always maintain it up!
I genuinely enjoy reading through on this site, it has fantastic content. “Beware lest in your anxiety to avoid war you obtain a master.” by Demosthenes.
Sweet blog! I found it while surfing around on Yahoo News. Do you have any tips on how to get listed in Yahoo News? I’ve been trying for a while but I never seem to get there! Cheers
FitSpresso: An Outline FitSpresso is a weight management formula made using five herbal ingredients.
I don’t even understand how I ended up right here, but I assumed this submit was good. I do not understand who you’re however definitely you’re going to a famous blogger in case you aren’t already 😉 Cheers!
I like the helpful information you provide in your articles. I’ll bookmark your blog and check again here regularly. I’m quite certain I’ll learn plenty of new stuff right here! Good luck for the next!
Good – I should certainly pronounce, impressed with your site. I had no trouble navigating through all tabs as well as related info ended up being truly simple to do to access. I recently found what I hoped for before you know it at all. Quite unusual. Is likely to appreciate it for those who add forums or something, web site theme . a tones way for your customer to communicate. Nice task..
Once I originally commented I clicked the -Notify me when new comments are added- checkbox and now each time a comment is added I get four emails with the same comment. Is there any method you’ll be able to take away me from that service? Thanks!
Would you be thinking about exchanging links?
Thank you for sharing with us, I conceive this website genuinely stands out : D.
great points altogether, you just gained a brand new reader. What would you suggest about your post that you made a few days ago? Any positive?
Saved as a favorite, I really like your blog!
I’m truly enjoying the design and layout of your blog. It’s a very easy on the eyes which makes it much more pleasant for me to come here and visit more often. Did you hire out a developer to create your theme? Exceptional work!
Thank you for the sensible critique. Me and my neighbor were just preparing to do some research on this. We got a grab a book from our area library but I think I learned more clear from this post. I am very glad to see such wonderful information being shared freely out there.
Hi there would you mind letting me know which webhost you’re utilizing? I’ve loaded your blog in 3 different browsers and I must say this blog loads a lot faster then most. Can you recommend a good hosting provider at a honest price? Cheers, I appreciate it!
Thanks, I have recently been searching for info approximately this subject for a long time and yours is the best I have found out till now. However, what in regards to the bottom line? Are you certain in regards to the supply?
Great write-up, I am regular visitor of one’s blog, maintain up the excellent operate, and It’s going to be a regular visitor for a long time.
I like this blog so much, saved to my bookmarks. “American soldiers must be turned into lambs and eating them is tolerated.” by Muammar Qaddafi.
You are a very bright person!
As soon as I observed this website I went on reddit to share some of the love with them.
Wow, fantastic weblog layout! How long have you been running a blog for? you make running a blog look easy. The entire look of your web site is fantastic, as well as the content!
I think you have noted some very interesting details, appreciate it for the post.
Exactly what I was looking for, regards for putting up.
Howdy! This is my 1st comment here so I just wanted to give a quick shout out and tell you I really enjoy reading your articles. Can you suggest any other blogs/websites/forums that go over the same subjects? Thank you!
I went over this site and I conceive you have a lot of wonderful information, saved to bookmarks (:.
Superb blog! Do you have any suggestions for aspiring writers? I’m planning to start my own site soon but I’m a little lost on everything. Would you advise starting with a free platform like WordPress or go for a paid option? There are so many choices out there that I’m completely confused .. Any suggestions? Cheers!
Appreciate it for helping out, wonderful info .
Thanx for the effort, keep up the good work Great work, I am going to start a small Blog Engine course work using your site I hope you enjoy blogging with the popular BlogEngine.net.Thethoughts you express are really awesome. Hope you will right some more posts.
I love it when people come together and share opinions, great blog, keep it up.
Definitely, what a fantastic blog and illuminating posts, I definitely will bookmark your site.Best Regards!
naturally like your web site but you need to check the spelling on quite a few of your posts. A number of them are rife with spelling problems and I find it very bothersome to tell the truth nevertheless I’ll surely come back again.
I am often to blogging and i really appreciate your content. The article has really peaks my interest. I am going to bookmark your site and keep checking for new information.
I like this post, enjoyed this one thanks for putting up.
Thanks for the update, can you make it so I get an update sent in an email whenever you write a fresh article?
Thank you for sharing excellent informations. Your web-site is very cool. I’m impressed by the details that you have on this site. It reveals how nicely you perceive this subject. Bookmarked this website page, will come back for more articles. You, my friend, ROCK! I found simply the info I already searched everywhere and just couldn’t come across. What a perfect website.
As a Newbie, I am permanently searching online for articles that can be of assistance to me. Thank you
Outstanding post, I believe website owners should larn a lot from this web site its really user pleasant.
I like this post, enjoyed this one regards for putting up.
Heya i am for the first time here. I came across this board and I find It truly useful & it helped me out much. I hope to give something back and help others like you helped me.
Would love to forever get updated great site! .
hello there and thank you for your information – I’ve definitely picked up anything new from proper here. I did then again experience a few technical points the use of this website, since I skilled to reload the site many occasions prior to I may just get it to load correctly. I had been brooding about in case your web hosting is OK? Not that I am complaining, but slow loading instances instances will very frequently affect your placement in google and could injury your high-quality score if advertising and ***********|advertising|advertising|advertising and *********** with Adwords. Well I am including this RSS to my e-mail and could glance out for much more of your respective interesting content. Make sure you replace this again soon..
I loved as much as you’ll receive carried out right here. The sketch is attractive, your authored subject matter stylish. nonetheless, you command get bought an shakiness over that you wish be delivering the following. unwell unquestionably come more formerly again since exactly the same nearly a lot often inside case you shield this hike.
Thank you for sharing superb informations. Your website is very cool. I am impressed by the details that you have on this site. It reveals how nicely you perceive this subject. Bookmarked this website page, will come back for more articles. You, my friend, ROCK! I found simply the info I already searched all over the place and simply couldn’t come across. What an ideal web site.
I want reading through and I believe this website got some really utilitarian stuff on it! .
hello there and thank you for your information – I’ve certainly picked up something new from right here. I did however expertise a few technical points using this website, as I experienced to reload the web site many times previous to I could get it to load properly. I had been wondering if your web hosting is OK? Not that I am complaining, but slow loading instances times will sometimes affect your placement in google and could damage your high-quality score if ads and marketing with Adwords. Well I am adding this RSS to my e-mail and can look out for much more of your respective exciting content. Make sure you update this again very soon..
Some really prime blog posts on this site, saved to bookmarks.
Howdy I am so thrilled I found your blog page, I really found you by mistake, while I was searching on Digg for something else, Regardless I am here now and would just like to say cheers for a incredible post and a all round thrilling blog (I also love the theme/design), I don’t have time to read through it all at the minute but I have saved it and also included your RSS feeds, so when I have time I will be back to read more, Please do keep up the fantastic job.
My brother recommended I may like this website. He used to be totally right. This post actually made my day. You cann’t believe simply how a lot time I had spent for this information! Thank you!
I like what you guys are up also. Such clever work and reporting! Carry on the superb works guys I¦ve incorporated you guys to my blogroll. I think it’ll improve the value of my site 🙂
you have a great blog here! would you like to make some invite posts on my blog?
You actually make it seem really easy together with your presentation but I to find this topic to be really something which I believe I might never understand. It seems too complicated and very large for me. I’m taking a look forward to your subsequent put up, I will attempt to get the dangle of it!
I’ve been absent for a while, but now I remember why I used to love this site. Thanks, I will try and check back more often. How frequently you update your web site?
What Is Wealth Signal? Wealth Signal isn’t just a financial tool; it’s a new way of thinking about and achieving wealth. Unlike traditional methods that focus on external strategies, Wealth Signal emphasizes changing your internal mindset.
Hiya! I simply want to give a huge thumbs up for the nice data you might have here on this post. I might be coming again to your blog for extra soon.
What is CogniCare Pro? CogniCare Pro is 100 natural and safe to take a cognitive support supplement that helps boost your memory power. This supplement works greatly for anyone of any age and without side effects
I got good info from your blog
Hello my family member! I wish to say that this article is amazing, nice written and come with almost all significant infos. I¦d like to look more posts like this .
Throughout the awesome pattern of things you’ll secure a B- with regard to effort and hard work. Exactly where you actually confused me personally was first on all the particulars. You know, they say, details make or break the argument.. And that could not be more accurate right here. Having said that, let me inform you just what did do the job. The text is highly persuasive which is probably the reason why I am taking the effort in order to opine. I do not really make it a regular habit of doing that. 2nd, although I can easily see a leaps in reasoning you make, I am not really convinced of exactly how you seem to connect the points which in turn make the final result. For the moment I shall yield to your position but wish in the foreseeable future you actually connect your facts much better.
I simply could not go away your site before suggesting that I really loved the usual info a person supply for your visitors? Is going to be again regularly in order to check out new posts.
You are a very smart individual!
Its good as your other content : D, thanks for putting up.
Hello there, I found your site via Google while looking for a related topic, your web site came up, it looks good. I have bookmarked it in my google bookmarks.
Wonderful web site. A lot of useful info here. I’m sending it to a few friends ans also sharing in delicious. And naturally, thank you for your effort!
Hiya, I’m really glad I have found this information. Nowadays bloggers publish just about gossips and web and this is really frustrating. A good blog with exciting content, this is what I need. Thank you for keeping this site, I’ll be visiting it. Do you do newsletters? Cant find it.
This is a genuinely excellent blog. Looking forward to more reads. Truly great!
Exceptional post however I was wondering if you could write a litte more on this topic? I’d be very thankful if you could elaborate a little bit further. Thank you!
I am not sure where you are getting your information, however great topic. I needs to spend a while finding out much more or understanding more. Thanks for great information I used to be looking for this information for my mission.
I like this post, enjoyed this one thanks for putting up. “When you make a world tolerable for yourself, you make a world tolerable for others.” by Anais Nin.
Do you have a spam problem on this website; I also am a blogger, and I was wanting to know your situation; we have created some nice methods and we are looking to exchange solutions with others, be sure to shoot me an e-mail if interested.
Keep functioning ,impressive job!
Some genuinely wonderful info , Gladiola I observed this.
I besides believe therefore, perfectly composed post! .
hello!,I like your writing very much! share we communicate more about your article on AOL? I need a specialist on this area to solve my problem. Maybe that’s you! Looking forward to see you.
Hello.This article was really fascinating, especially since I was looking for thoughts on this issue last Tuesday.
Everyone loves what you guys are usually up too. This type of clever work and coverage! Keep up the awesome works guys I’ve included you guys to blogroll.
Hi, Neat post. There’s a problem with your website in internet explorer, would test this… IE still is the market leader and a huge portion of people will miss your magnificent writing due to this problem.
Hello, i read your blog occasionally and i own a similar one and i was just wondering if you get a lot of spam comments? If so how do you stop it, any plugin or anything you can recommend? I get so much lately it’s driving me crazy so any support is very much appreciated.
Good – I should definitely pronounce, impressed with your web site. I had no trouble navigating through all tabs and related info ended up being truly easy to do to access. I recently found what I hoped for before you know it at all. Reasonably unusual. Is likely to appreciate it for those who add forums or something, site theme . a tones way for your customer to communicate. Excellent task.
Thanks for sharing excellent informations. Your web-site is very cool. I’m impressed by the details that you have on this website. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for extra articles. You, my friend, ROCK! I found just the info I already searched all over the place and simply couldn’t come across. What a perfect web site.
Spot on with this write-up, I actually suppose this website wants rather more consideration. I’ll most likely be again to learn much more, thanks for that info.
As soon as I discovered this site I went on reddit to share some of the love with them.
You actually make it seem so easy with your presentation but I find this topic to be actually something that I think I would never understand. It seems too complicated and very broad for me. I am looking forward for your next post, I will try to get the hang of it!
you are really a good webmaster. The site loading speed is incredible. It seems that you are doing any unique trick. In addition, The contents are masterpiece. you’ve done a magnificent job on this topic!
Enjoyed looking through this, very good stuff, appreciate it. “Golf isn’t a game, it’s a choice that one makes with one’s life.” by Charles Rosin.
I’d perpetually want to be update on new articles on this website , saved to favorites! .
You could definitely see your skills within the work you write. The arena hopes for even more passionate writers like you who are not afraid to mention how they believe. Always follow your heart.
Some genuinely nice stuff on this web site, I enjoy it.
Some genuinely superb posts on this web site, regards for contribution.
Some really quality blog posts on this website , saved to my bookmarks.
I like what you guys are up too. Such smart work and reporting! Keep up the superb works guys I have incorporated you guys to my blogroll. I think it will improve the value of my web site 🙂
so much excellent info on here, : D.
Hi! I’m at work surfing around your blog from my new iphone 3gs! Just wanted to say I love reading your blog and look forward to all your posts! Keep up the superb work!
I was just seeking this information for some time. After 6 hours of continuous Googleing, at last I got it in your site. I wonder what is the lack of Google strategy that do not rank this type of informative websites in top of the list. Usually the top web sites are full of garbage.
After study a few of the blog posts on your website now, and I truly like your way of blogging. I bookmarked it to my bookmark website list and will be checking back soon. Pls check out my web site as well and let me know what you think.
Excellent blog here! Also your website loads up fast! What web host are you using? Can I get your affiliate link to your host? I wish my website loaded up as quickly as yours lol
Hello there, I found your blog by means of Google even as looking for a comparable topic, your site got here up, it looks good. I have bookmarked it in my google bookmarks.
I was suggested this website by my cousin. I am not sure whether this post is written by him as no one else know such detailed about my trouble. You are incredible! Thanks!
Wohh precisely what I was looking for, thanks for putting up.
Hey there! Would you mind if I share your blog with my twitter group? There’s a lot of people that I think would really appreciate your content. Please let me know. Thanks
Good day! I could have sworn I’ve been to this blog before but after checking through some of the post I realized it’s new to me. Nonetheless, I’m definitely delighted I found it and I’ll be bookmarking and checking back frequently!
Hello! I just would like to give a huge thumbs up for the great info you have here on this post. I will be coming back to your blog for more soon.
I know this if off topic but I’m looking into starting my own weblog and was curious what all is required to get set up? I’m assuming having a blog like yours would cost a pretty penny? I’m not very web smart so I’m not 100 positive. Any tips or advice would be greatly appreciated. Thanks
This web site is really a walk-through for all of the info you wanted about this and didn’t know who to ask. Glimpse here, and you’ll definitely discover it.
Some really nice and useful info on this site, too I think the style has got good features.
You made some clear points there. I did a search on the subject and found most people will go along with with your blog.
You could definitely see your skills within the work you write. The world hopes for even more passionate writers like you who aren’t afraid to say how they believe. Always go after your heart. “What power has law where only money rules.” by Gaius Petronius.
I have been absent for a while, but now I remember why I used to love this blog. Thanks , I will try and check back more often. How frequently you update your website?
I like this weblog its a master peace ! Glad I detected this on google .
Hiya, I am really glad I’ve found this info. Nowadays bloggers publish just about gossips and internet and this is actually annoying. A good site with interesting content, that’s what I need. Thanks for keeping this site, I will be visiting it. Do you do newsletters? Can’t find it.
Hmm is anyone else encountering problems with the pictures on this blog loading? I’m trying to determine if its a problem on my end or if it’s the blog. Any suggestions would be greatly appreciated.
Keep working ,splendid job!
Good info. Lucky me I reach on your website by accident, I bookmarked it.
I was recommended this web site through my cousin. I am not certain whether or not this put up is written via him as no one else realize such distinctive about my difficulty. You’re wonderful! Thanks!
wonderful post.Ne’er knew this, thankyou for letting me know.
Throughout this grand scheme of things you secure a B+ for effort and hard work. Where you actually lost me personally ended up being on all the specifics. You know, as the maxim goes, details make or break the argument.. And it couldn’t be more correct right here. Having said that, let me say to you what exactly did deliver the results. Your text is definitely very convincing and that is possibly why I am making the effort in order to opine. I do not make it a regular habit of doing that. 2nd, whilst I can easily notice a jumps in reasoning you make, I am not necessarily sure of just how you appear to unite your details which help to make your conclusion. For now I will, no doubt subscribe to your issue but hope in the near future you actually link the facts better.
I like this post, enjoyed this one thanks for putting up.
I have been exploring for a little bit for any high-quality articles or weblog posts on this kind of space . Exploring in Yahoo I at last stumbled upon this website. Studying this information So i?¦m satisfied to convey that I’ve an incredibly excellent uncanny feeling I came upon exactly what I needed. I such a lot indubitably will make sure to do not disregard this site and provides it a look regularly.
Today, I went to the beach with my kids. I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She placed the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear. She never wants to go back! LoL I know this is completely off topic but I had to tell someone!
Oh my goodness! a tremendous article dude. Thank you Nevertheless I’m experiencing concern with ur rss . Don’t know why Unable to subscribe to it. Is there anybody getting equivalent rss problem? Anybody who knows kindly respond. Thnkx
Generally I don’t read post on blogs, but I wish to say that this write-up very forced me to try and do so! Your writing style has been surprised me. Thanks, quite nice post.
whoah this blog is great i love reading your articles. Keep up the great paintings! You recognize, many people are looking around for this info, you can help them greatly.
I have read some excellent stuff here. Definitely worth bookmarking for revisiting. I wonder how a lot effort you put to make one of these fantastic informative web site.
Valuable info. Lucky me I found your site by accident, and I’m shocked why this accident didn’t happened earlier! I bookmarked it.
Regards for all your efforts that you have put in this. very interesting information.
I really like your writing style, wonderful info, appreciate it for posting :D. “Faith is a continuation of reason.” by William Adams.
Incredible! This blog looks exactly like my old one! It’s on a entirely different topic but it has pretty much the same page layout and design. Outstanding choice of colors!
What Is Kerassentials? Kerassentials is a doctor-formulated oil for healthy skin and nails.
I’m often to blogging and i actually recognize your content. The article has actually peaks my interest. I’m going to bookmark your web site and keep checking for brand new information.
Some really quality content on this internet site, saved to my bookmarks.
Please let me know if you’re looking for a article writer for your weblog. You have some really good articles and I feel I would be a good asset. If you ever want to take some of the load off, I’d absolutely love to write some articles for your blog in exchange for a link back to mine. Please send me an e-mail if interested. Regards!
A lot of whatever you assert happens to be astonishingly legitimate and that makes me ponder the reason why I had not looked at this in this light before. Your article truly did switch the light on for me as far as this particular issue goes. Nonetheless at this time there is one particular issue I am not really too cozy with and while I attempt to reconcile that with the central idea of the issue, let me see just what the rest of the subscribers have to point out.Very well done.
Thanks for all your efforts that you have put in this. very interesting information.
Hello, Neat post. There is an issue with your site in web explorer, would check this… IE still is the marketplace leader and a big part of people will pass over your excellent writing because of this problem.
Everything is very open and very clear explanation of issues. was truly information. Your website is very useful. Thanks for sharing.
I’ve read some good stuff here. Certainly worth bookmarking for revisiting. I wonder how much effort you put to make such a great informative site.
Hey very cool blog!! Guy .. Beautiful .. Amazing .. I’ll bookmark your website and take the feeds also?KI’m happy to find so many helpful information here in the submit, we want develop more techniques in this regard, thank you for sharing. . . . . .
I don’t even understand how I finished up here, however I believed this submit used to be great. I don’t realize who you might be but certainly you’re going to a famous blogger if you happen to aren’t already 😉 Cheers!
Respect to post author, some good information .
Great post. I was checking continuously this blog and I’m impressed! Extremely helpful info specially the last part 🙂 I care for such information much. I was looking for this certain info for a very long time. Thank you and good luck.
Very interesting information!Perfect just what I was searching for!
I have learn some excellent stuff here. Certainly value bookmarking for revisiting. I wonder how much effort you put to make this sort of excellent informative website.
Great website! I am loving it!! Will come back again. I am taking your feeds also
Hello my loved one! I want to say that this article is awesome, great written and come with approximately all significant infos. I would like to see more posts like this .
Some truly excellent content on this website, thanks for contribution. “A religious awakening which does not awaken the sleeper to love has roused him in vain.” by Jessamyn West.
Hello There. I found your weblog the use of msn. That is a very neatly written article. I will be sure to bookmark it and return to learn more of your helpful information. Thank you for the post. I’ll definitely return.
I have learn a few good stuff here. Certainly price bookmarking for revisiting. I surprise how a lot effort you put to make one of these fantastic informative site.
Very interesting topic, thankyou for posting.
I think other web-site proprietors should take this site as an model, very clean and fantastic user friendly style and design, let alone the content. You’re an expert in this topic!
I believe this web site has got some really superb information for everyone :D. “Heat cannot be separated from fire, or beauty from The Eternal.” by Alighieri Dante.
I’ve been absent for a while, but now I remember why I used to love this blog. Thank you, I?¦ll try and check back more frequently. How frequently you update your website?
Pretty! This was a really wonderful post. Thank you for your provided information.
Thanks for one’s marvelous posting! I definitely enjoyed reading it, you may be a great author.I will be sure to bookmark your blog and will eventually come back sometime soon. I want to encourage yourself to continue your great job, have a nice weekend!
I have been absent for some time, but now I remember why I used to love this blog. Thanks , I will try and check back more frequently. How frequently you update your site?
I truly appreciate this post. I¦ve been looking all over for this! Thank goodness I found it on Bing. You have made my day! Thx again
I needed to compose you the very little word so as to thank you again about the precious tactics you’ve shown on this page. It’s really unbelievably generous with you to present without restraint just what numerous people could possibly have advertised for an e-book to get some dough for themselves, notably considering the fact that you might have done it if you ever desired. Those tricks additionally acted to become a fantastic way to realize that the rest have similar passion much like my very own to figure out a great deal more with respect to this condition. I think there are lots of more pleasurable times ahead for those who view your website.
Good – I should definitely pronounce, impressed with your site. I had no trouble navigating through all the tabs as well as related info ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Reasonably unusual. Is likely to appreciate it for those who add forums or something, site theme . a tones way for your client to communicate. Excellent task..
Hello, i read your blog from time to time and i own a similar one and i was just curious if you get a lot of spam remarks? If so how do you reduce it, any plugin or anything you can suggest? I get so much lately it’s driving me mad so any assistance is very much appreciated.
Fascinating blog! Is your theme custom made or did you download it from somewhere? A design like yours with a few simple tweeks would really make my blog jump out. Please let me know where you got your theme. Many thanks
whoah this weblog is excellent i really like studying your posts. Stay up the great paintings! You already know, a lot of individuals are hunting round for this info, you could help them greatly.
You are my aspiration, I have few web logs and sometimes run out from to post .
This is very fascinating, You are a very skilled blogger. I’ve joined your feed and look ahead to seeking more of your magnificent post. Additionally, I’ve shared your site in my social networks!
Hello. Great job. I did not anticipate this. This is a impressive story. Thanks!
Can I just say what a relief to find someone who actually knows what theyre talking about on the internet. You definitely know how to bring an issue to light and make it important. More people need to read this and understand this side of the story. I cant believe youre not more popular because you definitely have the gift.
Thanks for another fantastic post. The place else may anybody get that kind of information in such an ideal manner of writing? I’ve a presentation next week, and I’m at the look for such information.
Oh my goodness! an amazing article dude. Thanks Nevertheless I am experiencing situation with ur rss . Don’t know why Unable to subscribe to it. Is there anyone getting identical rss downside? Anybody who is aware of kindly respond. Thnkx
Hey very cool web site!! Man .. Beautiful .. Amazing .. I’ll bookmark your web site and take the feeds also…I am happy to find so many useful information here in the post, we need work out more strategies in this regard, thanks for sharing. . . . . .
he blog was how do i say it… relevant, finally something that helped me. Thanks
With havin so much content and articles do you ever run into any problems of plagorism or copyright violation? My website has a lot of unique content I’ve either authored myself or outsourced but it looks like a lot of it is popping it up all over the web without my agreement. Do you know any ways to help prevent content from being ripped off? I’d really appreciate it.
Thank you a lot for sharing this with all people you actually realize what you are speaking about! Bookmarked. Please additionally talk over with my site =). We will have a link trade agreement between us!
Whats Going down i am new to this, I stumbled upon this I have discovered It absolutely helpful and it has helped me out loads. I am hoping to give a contribution & help other users like its aided me. Great job.
Some genuinely wonderful info , Gladiolus I found this.
TOPSEO | Skaitmeninės rinkodaros agentūra Lietuvoje. Interneto svetainės reklama. Auditas. SEO optimizavimas. Efektyvūs darbuotojai
Its like you read my mind! You appear to know so much about this, like you wrote the book in it or something. I think that you can do with some pics to drive the message home a bit, but instead of that, this is magnificent blog. A fantastic read. I will certainly be back.
I appreciate your attention to detail in this blog post. Eager to read more of your work in the future.
I like the efforts you have put in this, thanks for all the great articles.
Have you ever thought about including a little bit more than just your articles? I mean, what you say is important and everything. However think of if you added some great visuals or video clips to give your posts more, “pop”! Your content is excellent but with pics and video clips, this website could definitely be one of the greatest in its field. Amazing blog!
I was very pleased to find this web-site.I wanted to thanks for your time for this wonderful read!! I definitely enjoying every little bit of it and I have you bookmarked to check out new stuff you blog post.
Hey, you used to write excellent, but the last few posts have been kinda boring?K I miss your super writings. Past several posts are just a little bit out of track! come on!
I in addition to my guys ended up looking through the best key points from the website and all of a sudden I got a horrible suspicion I had not expressed respect to the web site owner for those tips. All of the guys became consequently warmed to learn all of them and have now honestly been taking advantage of these things. Thank you for simply being really thoughtful as well as for using this form of perfect guides millions of individuals are really wanting to be informed on. Our honest apologies for not saying thanks to you earlier.
Hi there just wanted to give you a quick heads up. The words in your post seem to be running off the screen in Firefox. I’m not sure if this is a formatting issue or something to do with browser compatibility but I thought I’d post to let you know. The design look great though! Hope you get the problem fixed soon. Many thanks
Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful information. Thanks for the post. I will certainly comeback.
As a Newbie, I am continuously browsing online for articles that can benefit me. Thank you
Great tremendous issues here. I?¦m very satisfied to see your article. Thanks so much and i’m having a look forward to touch you. Will you please drop me a e-mail?
I am really inspired with your writing skills and also with the layout on your weblog. Is this a paid subject or did you modify it your self? Anyway stay up the excellent quality writing, it’s rare to peer a nice weblog like this one today..
I’m extremely impressed along with your writing talents as smartly as with the format to your weblog. Is that this a paid subject matter or did you modify it yourself? Anyway keep up the excellent high quality writing, it’s rare to peer a great weblog like this one these days..
Awsome website! I am loving it!! Will be back later to read some more. I am taking your feeds also
Some truly superb content on this internet site, thanks for contribution. “Better shun the bait, than struggle in the snare.” by John Dryden.
Very nice post. I just stumbled upon your blog and wanted to say that I’ve really enjoyed surfing around your blog posts. In any case I will be subscribing to your rss feed and I hope you write again soon!
Just wanna comment that you have a very nice internet site, I love the design and style it actually stands out.
You should take part in a contest for one of the best blogs on the web. I will recommend this site!
Hiya! I know this is kinda off topic however , I’d figured I’d ask. Would you be interested in trading links or maybe guest authoring a blog post or vice-versa? My site discusses a lot of the same subjects as yours and I feel we could greatly benefit from each other. If you might be interested feel free to shoot me an email. I look forward to hearing from you! Awesome blog by the way!
I simply couldn’t leave your site before suggesting that I actually loved the standard information a person provide for your guests? Is going to be back ceaselessly in order to investigate cross-check new posts
kolam4d link.
Would love to always get updated great web site! .
Hi there, i read your blog occasionally and i own a similar one and i was just wondering if you get a lot of spam remarks? If so how do you prevent it, any plugin or anything you can suggest? I get so much lately it’s driving me mad so any support is very much appreciated.
Hi! I just wanted to ask if you ever have any problems with hackers? My last blog (wordpress) was hacked and I ended up losing many months of hard work due to no back up. Do you have any solutions to stop hackers?
I admire your work, thankyou for all the interesting articles.
You should take part in a contest for one of the best blogs on the web. I will recommend this site!
Hey there! I’ve been following your weblog for a while now and finally got the courage to go ahead and give you a shout out from Humble Tx! Just wanted to tell you keep up the excellent job!
Thank you for the good writeup. It in fact was a amusement account it. Look advanced to more added agreeable from you! By the way, how could we communicate?
I love your blog.. very nice colors & theme. Did you create this website yourself? Plz reply back as I’m looking to create my own blog and would like to know wheere u got this from. thanks
It is really a nice and useful piece of info. I’m glad that you shared this helpful information with us. Please keep us informed like this. Thanks for sharing.
Hi my family member! I want to say that this post is amazing, great written and come with approximately all vital infos. I’d like to look extra posts like this .
Depiliacija vašku Klaipėdoje – tai puikus būdas pašalinti nepageidaujamus plaukelius. Procedūra buvo greita ir efektyvi, labai patenkinta rezultatu! Registruokis dabar.
You have brought up a very wonderful points, thankyou for the post.
Excellent blog here! Also your web site loads up very fast! What web host are you using? Can I get your affiliate link to your host? I wish my site loaded up as fast as yours lol
Woah! I’m really loving the template/theme of this blog. It’s simple, yet effective. A lot of times it’s very hard to get that “perfect balance” between user friendliness and visual appeal. I must say you have done a awesome job with this. Also, the blog loads super fast for me on Chrome. Exceptional Blog!
Good blog! I truly love how it is easy on my eyes and the data are well written. I am wondering how I might be notified whenever a new post has been made. I’ve subscribed to your RSS which must do the trick! Have a nice day!
Wohh precisely what I was looking for, thanks for putting up.
Thank you a lot for providing individuals with remarkably memorable opportunity to read from this web site. It really is very ideal and also full of fun for me and my office mates to visit your site at least 3 times in 7 days to find out the newest stuff you will have. And lastly, I’m just usually contented with all the good inspiring ideas you serve. Selected 1 areas in this article are truly the most beneficial I have ever had.
There are certainly lots of details like that to take into consideration. That could be a great level to convey up. I offer the thoughts above as general inspiration however clearly there are questions just like the one you convey up where crucial factor will be working in trustworthy good faith. I don?t know if greatest practices have emerged round things like that, but I’m sure that your job is clearly recognized as a fair game. Each boys and girls really feel the affect of only a second’s pleasure, for the remainder of their lives.
Hi there, I found your web site via Google while looking for a related topic, your site came up, it looks great. I have bookmarked it in my google bookmarks.
Terrific work! This is the kind of info that are supposed to be shared across the web. Shame on Google for now not positioning this post higher! Come on over and consult with my site . Thank you =)
Well I sincerely enjoyed reading it. This subject procured by you is very effective for correct planning.
Howdy just wanted to give you a quick heads up and let you know a few of the pictures aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different web browsers and both show the same outcome.
I like the efforts you have put in this, thanks for all the great articles.
I reckon something really special in this site.
I am continually browsing online for articles that can facilitate me. Thank you!
Thank you, I have recently been searching for information approximately this topic for ages and yours is the greatest I have came upon till now. However, what in regards to the bottom line? Are you certain about the source?
Thank you a lot for giving everyone an exceptionally spectacular opportunity to read from here. It is usually so fantastic and as well , full of fun for me personally and my office peers to visit your web site at minimum thrice every week to find out the latest items you will have. Of course, we are usually pleased for the brilliant guidelines served by you. Selected 1 points on this page are rather the simplest I have ever had.
Lovely just what I was searching for.Thanks to the author for taking his time on this one.
I’m still learning from you, but I’m trying to reach my goals. I certainly liked reading all that is written on your site.Keep the stories coming. I enjoyed it!
You got a very superb website, Gladiola I discovered it through yahoo.