Posted by This post talks about visualization of differential forms on differential manifolds. It is aimed at a reader who is in the process of learning about differential forms (or who already has), but who has not seen any visual intuition for what they are.
This post has as a prerequisite this post on the visualization of the dual of a vector space, which (hopefully) motivates a very simple particular case of what will be described in this post.
The references therein mentioned still apply, but mostly On the Visualisation of Differential Forms by Dan Piponi, on which most of this post is based.
This post is intended for purely illustrative purposes. We will not yet examine how this “formalism” is equivalent to the standard notion of differential form, nor will we turn our “proofs” and “definitions” into rigorous arguments. That is the content of a future post, in which we will show how the visualizations we will build here tie into the symbolic garbage usually called “tensor algebra”.
Differential Forms
In all that follows, $M$ denotes an $n$-dimensional smooth manifold, for some non-negative integer $n$.
Motivation ($n$-form)
Before defining the notion of differential form, it is first useful to consider what problem we intend to solve.
The problem at hand is that of integration. We already know how to differentiate maps between differential manifolds, and now we wish to find out how to integrate them. Unfortunately, by itself this is not possible.
For example, consider the constant function equal to one on the unit sphere $S^1$. Its integral really ought to be the surface area of the sphere, $4\pi$. On the other hand, the unit sphere is diffeomorphic, and therefore indistinguishable as a smooth manifold, from the radius two sphere, which we will call $2S^1$. But integrating $1$ on the latter yields a different result: $16\pi$. What gives?
The obvious answer is that we shouldn’t be integrating the 1 function, but rather the $\frac14$ function, because the diffeomorphism between $S^1$ and $2S^1$ “spreads out the function”. And while this is legitimate intuition, that’s just not how functions “go across diffeomorphisms”. We need to consider some other kind of object.
Let’s inspect the “physicist’s way” of approaching integration. First, one divides the domain of discourse into many small rectangles, whose area we know how to calculate. Then, for each square, one multiplies the value of $f$ on that rectangle by its area $\dl A$. Finally, one sums over all the tiny squares, which we represent by a tall S in a familiar way as $\int f \dl A$.
How does this “approach” fail on smooth manifolds? The problem is that we don’t know how to measure the areas of the tiny rectangles. Indeed, the notion of area is not conserved when we change charts, so we cannot simply “measure the area of the rectangle in coordinates”, because this area depends on the coordinates chosen.
Consequently, in order to define integration, we need to add additional structure. For each point $x$ in our manifold $M$, we need to know how to measure areas of tiny rectangles in a coordinate-free way. The apparatus that allows us to do so is precisely the differential form: it receives an “infinitesimal parallelogram” (represented by its edges given as tangent vectors) and returns its area (or rather, its area “scaled up” as not to be infinitesimal).
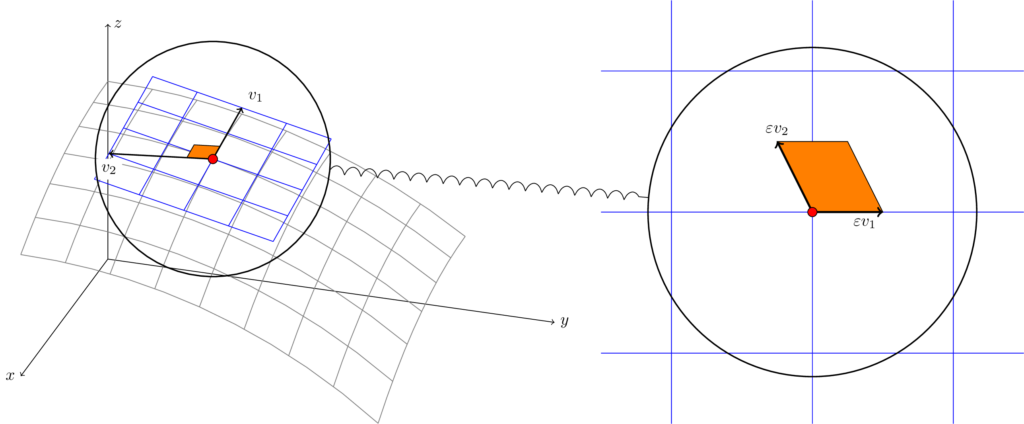
This, by itself, is enough motivation to define a differential form as “something that takes $n$ tangent vectors and returns a number”, and it is very natural to require multilinearity and skew-symmetry. However, we have not yet reached a useful visualization.
To proceed, let us imagine that our manifold is some kind of physical object, composed of many tiny pieces like “atoms”. Then, there is an unambiguous way to measure some kind of area on the manifold: given some shape, one can count how many atoms lie in this shape. Then, assuming the atoms are uniformly distributed in some sense, one must only multiply the atom count by some scaling factor to obtain “the area” of the shape.
This thought experiment shows that a “manifold made of atoms” has a canonical way of measuring area (modulo a scaling factor). Therefore, it might be worth toying with the idea of representing a differential form by “a cover of the manifold by atoms”.
We then make the following “definition”: a differential form on $M$ is a cover of $M$ by an infinitely dense mesh of points. To calculate the area of a set $A \subseteq M$, we count the number of atoms in $A$, and multiply by an appropriate infinitesimal number.
The biggest benefit of this point of view is that it behaves naturally with regard to rescalings. In other words, if we apply a diffeomorphism to the manifold that scales everything up in some manner, we are also scaling up the spaces between the atoms (but not the weight of the atoms themselves!). Therefore, area is conserved.
Equivalently, this point of view allows for coordinate-independent measurement of area, as any distortion between two charts of $M$ will imply an equal distortion of the “atoms”, and again area is conserved
Other Order Forms
Now that we have solved the problem of area measuring, what comes next? Why are other dimension forms necessary?
At the most elementary level, forms of dimensions other than $n$ appear in the statement of the generalized Stokes theorem (we will henceforth drop the “generalized” from the name). This is an important theorem, having as particular cases the divergence and Green’s theorem, which are very useful tools of calculation. Therefore, I hope the reader will agree that the study and proof (“proof”) of this theorem is a worthwhile endeavor.
If the reader is not yet familiar with the Stokes theorem, they may have some trouble understanding the following few paragraphs. However, I hope that the subject matter will become clearer over time. In any case, I suggest that such a reader would continue linearly until we state and “prove” the Stokes theorem, and then return here and reread this part with more context.
The statement of the Stokes theorem relates the integral of a form $\omega$ on the border of a set $U$ with the integral of its “derivative” $\dl \omega$ on the interior of $U$, with the usual statement being cleanly written as
\[\int_{\partial U}\omega = \int_U \dl \omega.\]
Setting aside for now the “derivative” part of the statement, there is something we first have to touch. What kind of object does $\omega$ have to be for us to integrate it on $\partial U$? It cannot be a differential form as we have described them, because if we fill the space $M$ with a very fine grid of atoms, it is very unlikely that any of them lie exactly on the border of $U$.
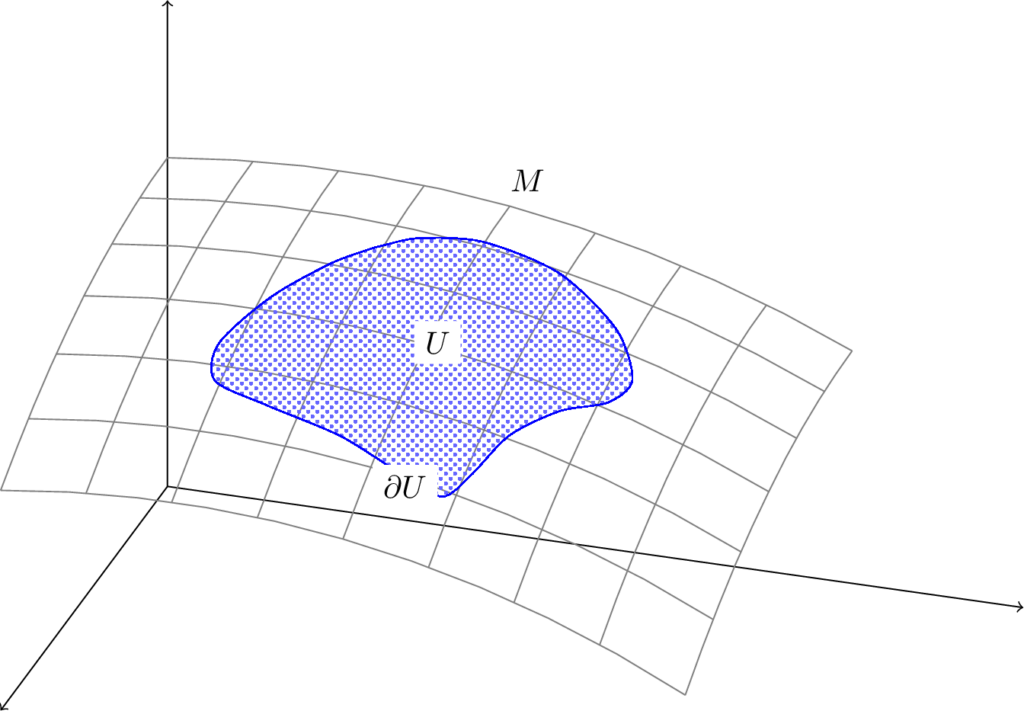
In other words, we seek to solve the following problem. We have already concluded that the kind of object used to integrate over $n$-dimensional sets and measure $n$-dimensional area is “covers of the space with points”. However, this is not adequate to integrate over $k$-dimensional sets, with $k < n$, i.e. $k$-dimensional submanifolds of $M$. Therefore, we wish to discover what kind of object will allow us to naturally define integrals on $k$-dimensional submanifolds of $M$.
From now on, let $N$ be a $k$-dimensional submanifold of the $n$-dimensional manifold $M$.
The algebraic point of view presents itself rather naturally. Recall that the algebraic definition of a differential form is a thing that takes $n$ tangent vectors to the same point and returns a number. We want to define an object on $M$ which can be “restricted to $N$”, becoming an object which takes $k$ vectors tangent to $N$ and returns a number. It is then natural to define a “$k$-form on $M$” as an object $\omega$ which takes $k$ tangent vectors at the same point of $M$, and the restriction to $N$ becomes simply the restriction of $\omega$ to the collection of vectors tangent to $N$.
Let us now go from the algebraic point of view to the pictorial one. A $k$-form receives $k$ vectors, forming the edges of an infinitesimal parallelogram of dimension $k$. For example, if $n = 3$, this means that we are considering an infinitesimal line segment or rectangle, instead of a cube.
If you’ve seen my other post on the dual space, you should already be familiar with a way to visualize a covector, a thing that receives a vector and returns a number, as a collection of hyperplanes. This carries over to the notion of 1-form, which is also a thing that recieves a vector and returns a number. Indeed, we can visualize a 1-form $\eta$ as a collection of hypersurfaces (surfaces of dimension $n-1$) on our manifold, and evaluating $\eta$ on a vector consists of counting how many of these hypersurfaces intersect the given vector. Note the similarities:
| $n$-form $\omega$ | 1-form $\eta$ |
|---|---|
| Collection of points (0-dimensional) | Collection of hypersurfaces ($n-1$-dimensional) |
| To evaluate on a collection of vectors, count how many points are in the parallelogram spanned by them | To evaluate on a vector, count how many hypersurfaces intersect it |
Now, it may not be obvious with only two data points, but I propose the following visualization of the intermediate steps: Visualize a $k$-form as a collection of $n-k$-planes.
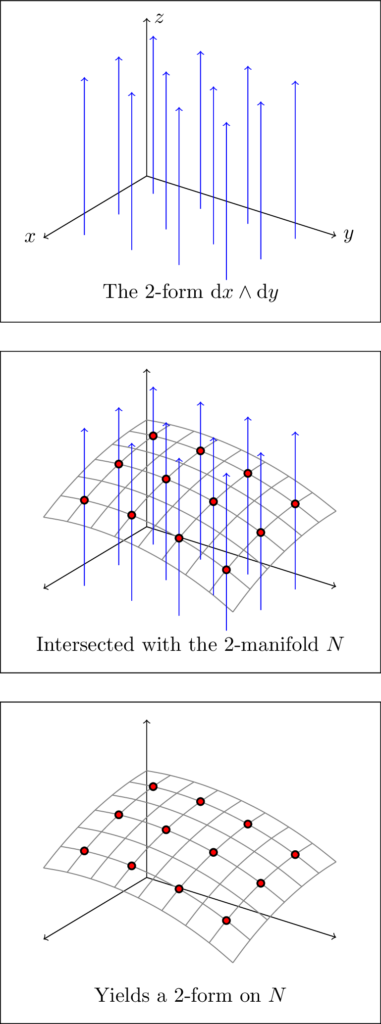
Under this visualization, to evaluate such a $k$-form $\omega$ on a collection of $k$ vectors is to count how many of these $n-k$-planes intersect the $k$-parallelogram spanned by these vectors. The dimensions check out: in general, the intersection between two objects of dimension $a$ and $b$ is an object of dimension $a+b-n$, and if $a = n-k$ and $b = k$, this means that these intersections will often be 0-dimensional points.
As a bonus, our original goal is also met. Indeed, if the $k$-form $\omega$ consists of covering the space in $n-k$-planes, the restriction of $\omega$ to a submanifold $N$ consists simply of taking the intersection between these planes and $N$. As in the previous paragraphs, these intersections will often be points, and so we recover a differential form (of dimension $k$) on $N$.
The Bad and the Ugly
There are two big details we have been neglecting, and will keep neglecting, over the course of this post. We will now take a slight detour, to shed some light on them before we shove them under the carpet again.
Readers who are not terribly interested are encouraged to skip ahead to “The Exterior Derivative”.
Transversality and Perturbations
Let’s go back to this paragraph: “in general, the intersection between two objects of dimension $a$ and $b$ is an object of dimension $a+b-n$, and if $a = n-k$ and $b = k$, this means that these intersections will often be 0-dimensional points.” Why would this statement be true, and what do we mean by “in general”?
The answer is related to a concept known in differential geometry as transversality. The following discussion comes with a lot of asterisks, and is even more handwavey than the rest of this post.
Two submanifolds $A$ and $B$ of a common manifold $M$ are said to intersect transversely at a point $p$ if $T_p A$ and $T_p B$ span $T_p M$. Intuitively, this corresponds to the intersection being, well, transversal, as opposed to tangent. For example, two curves in the plane intersect transversely at a point if they form an angle which is not 0 or 180 degrees. Two curves in space never intersect transversely.
The most important fact about transversality, aside from the fact that transverse intersections are The Nice Kind, is that it is robust and very common. By this we mean that if two manifolds intersect transversely, then small enough perturbations of the manifolds will not mess that up: given small enough perturbations, they will still intersect, and the intersection will still be transverse.
Furthermore, non-transversality is sensitive and rare. If two manifolds intersect non-transversely, then almost no perturbations will preserve this state of affairs. For example, consider two lines in space. If you perturb either of them randomly, it is almost certain that they will stop intersecting. As another example, consider in $\R^2$ the $x$ axis and the graph of $f(x) = x^3$. These curves intersect non-transversely at the origin, but any tiny nudge in either of these curves in the up or down direction will make the intersection transverse.
Finally, transverse intersections satisfy the dimensionality property referred at the start. That is, if two manifolds $A$ and $B$, of dimension $a$ and $b$ respectively, intersect transversely, their intersection is a manifold of dimension $a+b-n$.
As a consequence, we will henceforth (as we have thus far) ignore the possibility of nontransverse intersections.
Orientations
Another important detail to be observed is the orientation of the surfaces “composing” a form, and more specifically the orientation of the intersections.
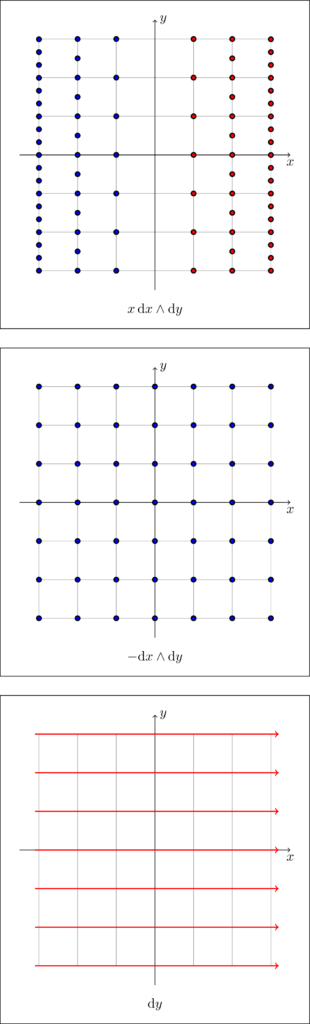
For example, consider the example representation of the form $x \dl x \wedge \dl y$ pictured above, or something even simpler such as $-\dl x \wedge \dl y$, both in $\R^2$. Then, the “atom” representation requires that some or all of the atoms composing these representations count negatively.
As another example, consider, still in $\R^2$, the 1-form $\dl y$, which is represented as a uniform stack of horizontal lines. The mnemonic “to calculate $\dl y (v)$ is to count how many horizontal lines $v$ crosses” works if $v$ is pointing upwards, but requires negating the result if $v$ points downwards.
The easiest solution is to play with orientability. Suppose, for the moment, that $M$ is oriented, and let $\omega$ be a $k$-form. Then, we make the following slight addendum to our visualization of $\omega$: we represent it visually by a mesh of oriented $n-k$-submanifolds.
Here’s what this means for visualization purposes:
- Points will be represented, as we have so far, as either red or blue depending on whether they are positively or negatively oriented. (Yes, a zero dimensional manifold has orientation, either positive or negative at each point!)
- Curves will be represented with an arrow representing the positive direction. The sign convention for evaluation will be given by the right-hand rule, so for example $\dl y$ in $\R^2$ would be given by arrows pointing to the right, and $\dl x \wedge \dl y$ in $\R^3$ would be given by arrows pointing upwards.
- When representing 1-forms in $\R^3$ via surfaces, it should be understood which normal direction is positive, either via arrows indicating the positive direction or through written indication. However, this case probably won’t happen a lot.
- Since I’m not going to be making pictures in 4d, that basically exhausts all possible cases, except for the case of 0-forms, which will be mentioned at the end.
Again, note that all of this makes sense for orientable $M$. In one hand, this foreshadows an interesting fact: the theory of forms is more well-behaved for orientable manifolds than non-orientable ones. For example, a Riemannian metric on $M$ induces a volume form if and only if $M$ is orientable; in fact, a differentiable manifold $M$ is orientable if and only if it admits an $n$-form which is never null. Finally, and most problematic, the definition of integral of an $n$-form on a manifold requires that the manifold be orientable, so without orientability everything we intend to do with forms breaks down. [Note: There is a way around this last problem called “densities”, which is a sort of generalization of $n$-forms. Unfortunately, I know nothing about it.]
On the other hand, I would like to point out that despite these problems, a lot of what we will do works equally well in non-orientable surfaces. Indeed, every manifold is locally orientable, so our pictures work locally, and non-orientability will not invalidate our discussions on the exterior derivative, wedges or Lie derivatives. As a rule of thumb, local or pointwise statements will work in every manifold, while global statements require orientability.
The Exterior Derivative
Recall the form $\dl y$ on $\R^2$, which can be represented as a collection of horizontal lines. A trivial modification to this form would be considering $y \dl y$, in which the lines are getting denser the further up you go.
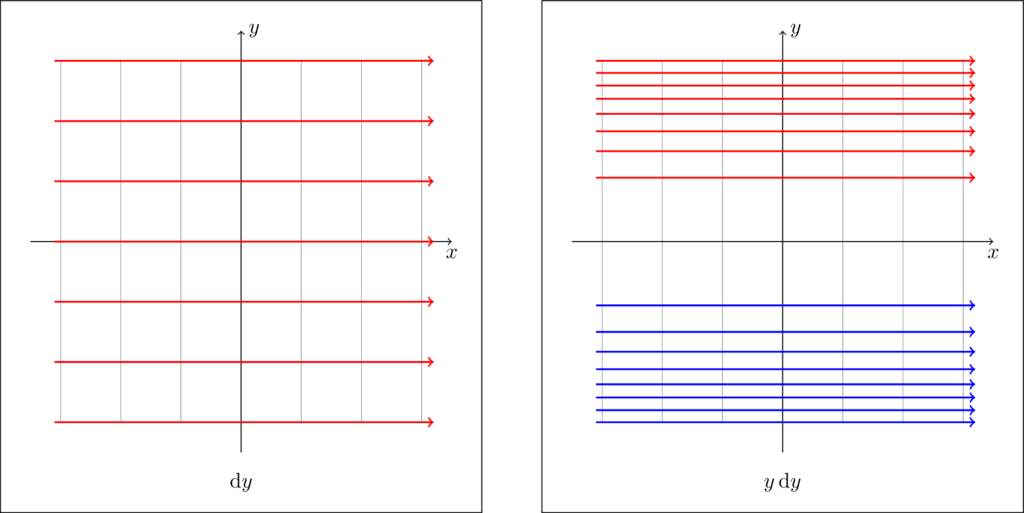
A slightly less trivial modification would be the form $x \dl y$. In this case, the lines are getting denser the further to the right you go, yet the lines must be horizontal, in order for horizontal vectors to intersect none of them. Consequently, you get a new-looking picture:
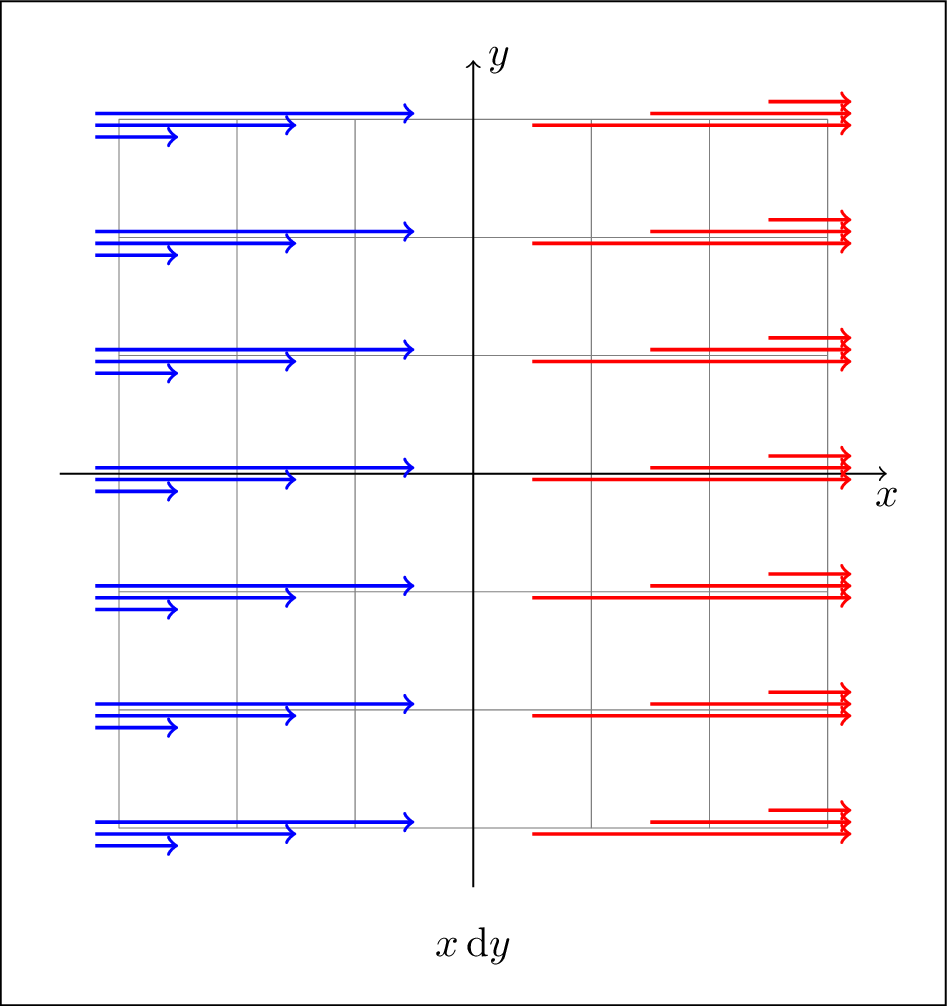
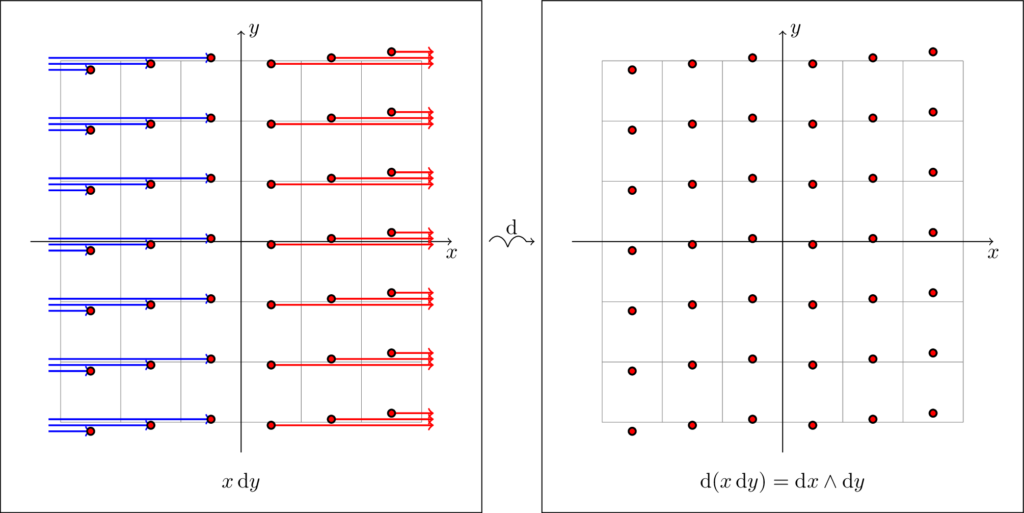
The new phenomenon exhibited here is the “creation of lines”. This phenomenon is meaningless for $n$-forms, but for forms of other dimensions $k$ it is the distinction between the “atoms” being $n-k$-manifolds, versus being $n-k$-manifolds with boundary.
All this to say, our formalism does not require that the surfaces representing forms be boundaryless. Indeed, some forms, like $x \dl y$, require that the surfaces representing them have boundary. As a consequence, it is natural to ask, given a form, whats its boundary is. You can probably see where this is going: if the $k$-form $\omega$ is represented by a collection of $n-k$-surfaces, their boundaries (which are $n-(k+1)$-forms) make up a $k+1$-form which we usually denote $\dl \omega$.
Let’s see what this looks like in the above examples. The forms $\dl y$ and $y \dl y$ are represented without boundary, so their exterior derivatives are null, which agrees with the symbolic computation. On the other hand, if we look at the borders of $x \dl y$, we get a uniform mesh of points, also known as the familiar $\dl x \wedge \dl y$.
Let’s look at another, more complicated example, now in three-dimensional space.
Consider the 1-form $xy \dl z$. As in the $x \dl y$ example, this form must be represented by horizontal planes. Their density depends on $x$ and $y$, so that near the axes there are less planes, and far from the axes there are more. Furthermore, the amount of planes at a point is proportional to $xy$, so it makes sense to represent this form by a collection of planes with hyperbolic borders:
Let us now compute visually the 2-form $\dl(xy \dl z)$. The picture is as follows.
The result is a collection of curves satisfying the equation $xy = c$, with $z$ constant. Let us label these curves by $c$ and $z$. We will calculate the form $\dl(xy \dl z)$, let us call it $\omega$ from now on, at a point $p = (x_0,y_0,z_0)$.
We’ll revisit this example again when we look at the wedge product, but until then we will sketch the answer by calculating it for a well-chosen basis of the tangent space at $p$. Consider the following three vectors:
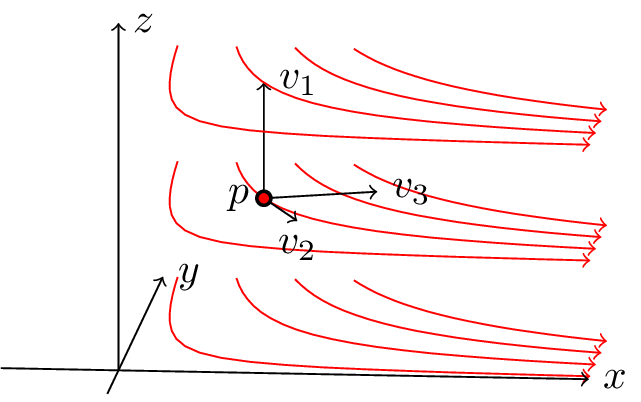
The vector $v_1$ is simply $(0,0,1)$. The vector $v_2$ is chosen to be tangent to the curves, and $v_3$ is meant to point in a direction of “increasing $c$”. We’ll look at $\omega(v_1, v_3)$ shortly, but until then it should be clear that $\omega(v_1,v_2) = \omega(v_2,v_3) = 0$. In general, whenever a vector is tangent to the curves defining a form, any parallelogram with it as an edge will have no (or negligible) intersection with these curves.
With only this, we are in position of finding a partial expression for $\omega$. Indeed, if $a_1, a_2, a_3, b_1, b_2, b_3$ are real numbers,
\[\omega(a_1 v_1 + a_2 v_2 + a_3 v_3, b_1 v_1 + b_2 v_2 + b_3 v_3) = \left\lvert \begin{matrix}a_1 & b_1 \\ a_3 & b_3 \end{matrix} \right\rvert \omega(v_1, v_3).\]
It remains to compute $a_1$ and $a_3$ for a vector of the form $a= a_1 v_1 + a_2 v_2 + a_3 v_3$.
The $a_1$ component is trivial: it is simply the $z$ component of $a$. To compute $a_3$, it is convenient to calculate $v_3$. If $v_1$, $v_2$ and $v_3$ are chosen to make an orthonormal basis, $a_3$ can be easily written as $a_3 = a \cdot v_3$.
First, we compute $v_2$. Since it is tangent to horizontal curves, it is of the form $(v_{2x}, v_{2y}, 0)$. Since it is tangent to the curve $xy = c$, the value of $c$ for $p + \varepsilon v_2$ ought to be equal to $x_0 y_0$ to first order. This value is $(x_0 + \varepsilon v_{2x})(y_0 + \varepsilon v_{2y}) \approx x_0 y_0 + \varepsilon (x_0 v_{2y}+ y_0 v_{2x})$. Therefore,we conclude
\[x_0 v_{2y}+ y_0 v_{2x} = 0.\]
The unit norm solution to this equation with, say, $v_{2x} > 0$, is
\[v_2 = \frac1r (x_0, -y_0, 0), \quad r = \sqrt{x_0^2 + y_0^2}.\]
Finally, we calculate $v_3$ as a unit vector, pointing away from the axes, orthogonal to $v_1$ and $v_2$.
Orthogonality to $v_1$ means simply its last coordinate is null, so we get $v_3 = (v_{3x}, v_{3y}, 0)$. Orthogonality to $v_2$ means $x_0 v_{3x}-y_0 v_{3y} = 0$, with obvious solution
\[v_3 = \frac1r (y_0, x_0, 0).\]
In conclusion, we may write
\[\omega(a, b) = \left\lvert \begin{matrix}a_z & b_z \\ \frac1r (y_0 a_x + x_0 a_y) & \frac1r (y_0 b_x + x_0 b_y) \end{matrix} \right\rvert \omega(v_1, v_3),\]
Or, in more familiar wedge notation,
\[\omega = \omega(v_1, v_3) \dl z \wedge \left( \frac1r ( y_0 \dl x + x_0 \dl y) \right) = \frac1r \omega(v_3, v_1) \left( y_0 \dl x \wedge \dl z + x_0 \dl y \wedge \dl z \right). \]
(Note the double sign change in the second step! $\omega(v_1,v_3) \to \omega(v_3,v_1)$ and $\dl z \wedge \dl x \to \dl x \wedge \dl z$.)
Finally, we calculate $\omega(v_3, v_1)$. The order change may appear confusing (we put $v_3$ before $v_1$), but it is actually for the best: this way, the vectors $v_3, v_1$ and the red arrows satisfy the right-hand rule, so that the result is positive.
Since $v_1$ is a vertical unit vector and the system is symmetric with regard to vertical translations, we reduce the computation to finding out how many curves the vector $v_3$ passes through in the $z = z_0$ plane. In other words, we wish to find out how much $c$ varies between $p$ and $p + \varepsilon v_3$. The answer is trivial to calculate:
\[c_{\text{final}} = (x_0 + \varepsilon \frac1r y_0)(y_0 + \varepsilon \frac1r x_0) \approx c_{\text{start}} + \varepsilon \frac1r (x_0^2 + y_0^2) = c_{\text{start}} + \varepsilon r.\]
Therefore, we conclude that the rectangle spanned by $\varepsilon v_3$ and $\varepsilon v_1$ passes through roughly $\varepsilon^2 r$ curves, whence $\omega(v_3, v_1)$ should be $r$, and so our sketches yield
\[\omega = y \dl x \wedge \dl z + x \dl y \wedge \dl z.\]
That was a boatload of work. Good thing they invented vector calculus, with which we may verify our computation:
\[\omega = \dl(xy \dl z) = \dl(xy) \wedge \dl z = (y \dl x + x \dl y) \wedge \dl z = y \dl x \wedge \dl z + x \dl y \wedge \dl z.\]
The Stokes Theorem
In this framework, the Stokes theorem is quite a triviality. (If you consider something like the Jordan curve theorem a triviality, at least…)
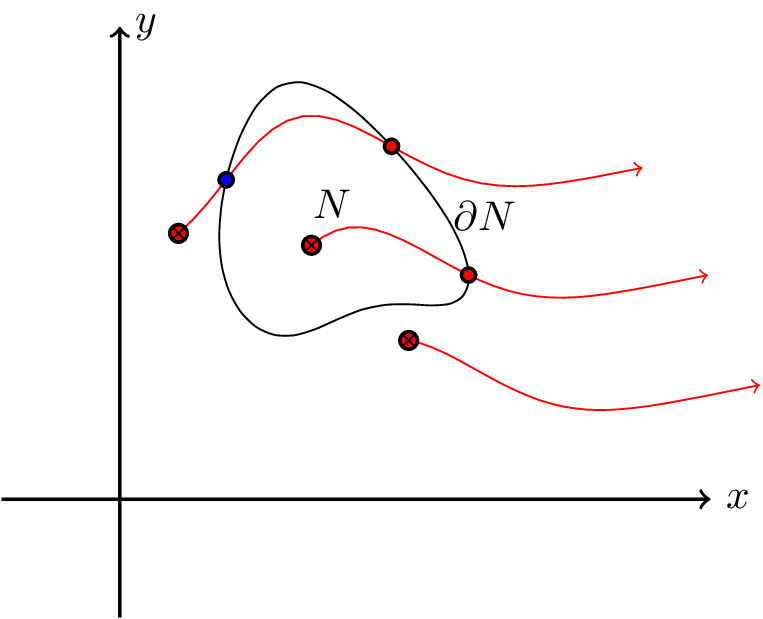
Intuitively, let $M$ be an $n$-dimensional manifold and $Q$ a manifold which splits $M$ into “an inside” and “an outside”. The “inside” must be small in the sense that a line cannot “go on infinitely inside”. For example, the plane $z = 0$ would not split $\R^3$ into an inside and an outside, because neither half-space is small in this sense: you have infinite line segments living in each.
An example of a set we wish to consider is $Q = S^2$, which splits $\R^3$ into an inside and an outside. The inside is “small” because the only way to have an infinite line inside $Q$ is to have it wind up infinitely. Now, it is hard to express properly why such infinite winding up is disallowed, but if we assume that it is, then the inside of $S^2$ counts as small. We are interested in sets whose inside satisfies this property.
Of course, all this intuitive handwaving is intended to convey a concept which mathematicians have figured out long ago: We want $Q$ to be the border of a manifold with boundary, say $N$. To say that $N$ (“the inside”) is small is to say that $N$ is compact.
Now, we intend to integrate some $n-1$-form $\omega$ on $Q$. Ordinarily, there would be no reason to believe that there would be a way to simplify this computation, but the hypothesis that $Q$ splits the space in two implies a very important fact: any line which enters $Q$ must either exit it again or stop inside $Q$. Therefore, if we see integrating an $n-1$-form on $Q$ as counting the lines entering $Q$, we conclude that solving the problem of integrating $\omega$ on $Q$ is the same as to count the number of line ends in $N$. The line ends are counted by $\dl \omega$, and so we conclude the familiar formula
\[\int_{\partial N}\omega = \int_N \dl \omega.\]
What Comes Next
Let’s recap what we’ve done thus far. We have defined an $n$-form as an area/volume/measure measuring device. In order to measure areas of lower dimension (say, on submanifolds) we have defined the notion of $k$-form for $k < n$. These lower-dimensional forms displayed a phenomenon that could not be seen in the $n$-forms, which is the possibility that the “atoms” were manifolds with boundary. Hence, we defined the notion of exterior derivative as that which recovers these boundaries, and turns a $k$-form into a $k+1$-form. Finally, we exploited the notion of “closed surface” to simplify the computation of integrals of $n-1$-forms, by noticing that counting outbound lines is the same as counting line ends inside the surface. This is the celebrated Stokes Theorem.
The Stokes Theorem is certainly a very important milestone in vector calculus, but it is only the beginning. I cannot hope to describe every phenomenon and definition, but in the remainder of this post we will look at four important concepts: Wedge Products, Pullbacks, Lie Derivatives and Inner Products (aka Contraction aka that thing where you put a vector field into the form). The discussion will culminate in another celebrated formula of tensor calculus: Cartan’s Magical Formula
\[ \Lie_X(\omega) = \dl(X \into \omega) + X \into \dl \omega.\]
The Wedge Product
Introduction: Wedges as Symbolic Glue
One of the biggest advantages of tensor calculus is its practicality. With only a small set of rules, it is possible to do all kinds of manipulations and calculations in coordinates, which is part of what makes tensors so useful and applicable in engineering and physics.
The reason behind this practicality is that, as the reader may or may not already know, tensors are decomposible into very elementary parts. Indeed, any tensor can be written using only functions and one-forms, for example something of the sort
\[\omega = f \dl x \wedge \dl y + g \dl z \wedge \dl w.\]
The symbol between the one-forms is called the wedge product, and it is the glue that allows us to compose small-dimensional forms in order to make higher-dimensional forms.
Therefore, when we define some new type of transformation (like, say, an exterior derivative or a Lie derivative), it suffices to find how it behaves on these elementary parts, and how it behaves under the wedge product. This then gives us a recipe for computing that transformation: simply decompose, apply to the elementary parts, and tie it all back again.
[Remark: The reader might (understandably) believe that there is not one type of “symbolic glue” in play, but two: the wedge product, and the product by scalar functions. However, as it turns out, the product by a scalar function actually corresponds to the wedge product by a zero-form; see appendix A for details.]
Wedges as Intersections
Our current goal is to decompose a $k$-form into forms of lower dimension. From the perspective of our framework, in which a $k$-form is represented by $n-k$-dimensional surfaces, we wish to write a manifold in terms of manifolds of higher dimension.
This may seem abstract, but it is very easy to motivate if we think in terms of cartesian equations. For example, consider a one-dimensional curve in $\R^3$ such as the red circle in the following figure:
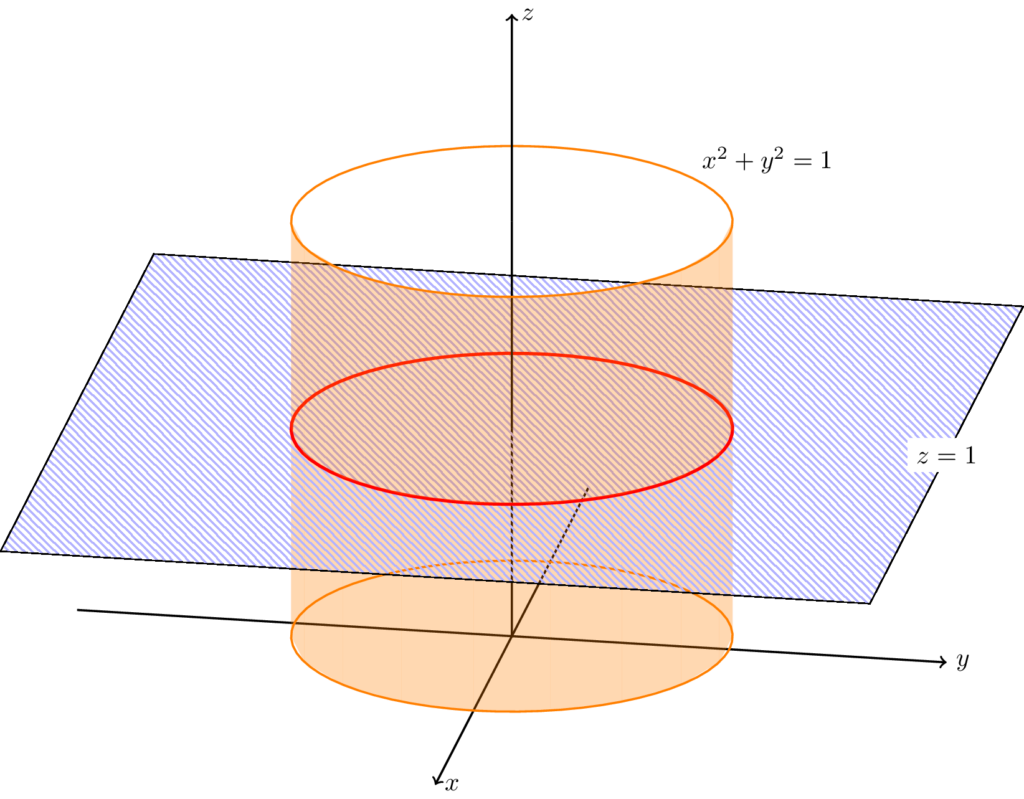
This curve can be written in terms of the cartesian equations
\[\begin{cases} x^2 + y^2 = 1,\\z = 1.\end{cases}\]
Now there is a trivial way to decompose this one-dimensional object as the intersection of two 2-dimensional objects: a horizontal plane $z=1$ and a cylinder $x^2 + y^2 = 1$.
This is a more or less general phenomenon. We can define a $d$-dimensional surface in $n$-dimensional space through $n-d$ cartesian equations. Each of these equations separately defines an $n-1$-dimensional surface, and their intersection is obviously the surface we started with. In other words, we get a kind of general principle:
A surface $S$ of dimension $d$ contained in $n$-dimensional space can be written as the intersection of $n-d$ hypersurfaces.
The next step is to apply to this to our framework for forms. A $k$-form $\omega$ is represented through $n-k$-surfaces, so we should expect to write the surfaces composing $\omega$ as the intersection of $k$ hypersurfaces; that is, to write $\omega$ in terms of $k$ one-forms. Sound familiar?
This, in turn, presents a way to “glue forms”: take the intersection of the corresponding surfaces. Indeed, the notation of wedge product is even suggestive: ever notice how $\omega \wedge \eta$ kind of looks like $\omega \cap \eta$? I have no idea if this is a coincidence, but if so it is a very fortunate one.
Let $\omega$ be a $k$-form and $\eta$ be an $\ell$-form. Define the wedge product of $\omega$ and $\eta$ as the $k+\ell$-form whose atoms are the pairwise intersections of atoms from $\omega$ and atoms from $\eta$.
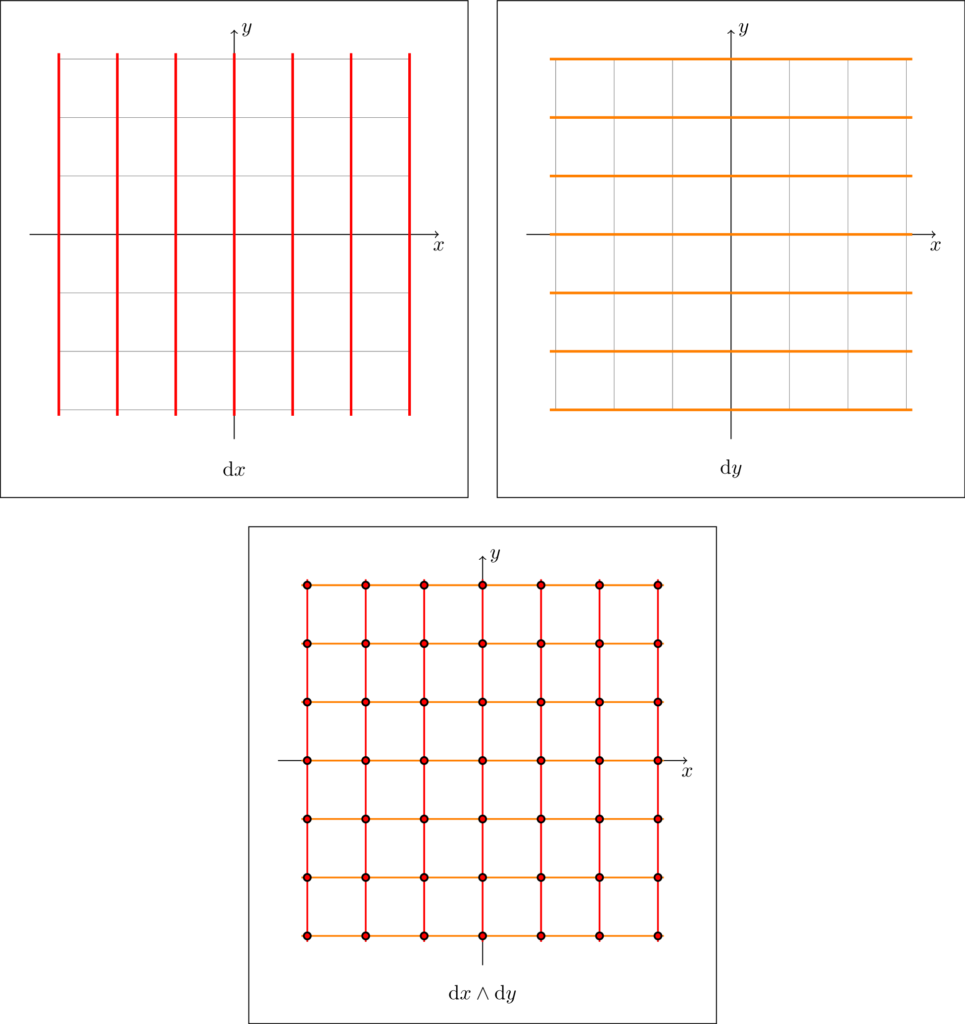
For a simple example, let us show that the wedge product $\dl x \wedge \dl y$ corresponds to the uniform mesh of points we have come to associate with the standard area form on $\R^2$. Indeed, recall that $\dl x$ is represented by uniformly spaced vertical lines, and $\dl y$ is represented by uniformly spaced horizontal lines. Then, it is visually obvious that the collection of pairwise intersections is a square grid of points.
Dimensions, Orientations and Properties
Appealing though this “definition” of wedge product may be, it remains to show (or at least, plausibly convince) that the wedge product has the properties we have come to expect it to have. For example, is it even obvious that the dimension of the wedge is the sum of the dimensions of the arguments? In this section, we sketch arguments to justify the most important properties of the wedge product.
- Dimension: First, we recall the discussion on transversality above. In particular, recall that we will always be assuming that all intersections are transverse, which bodes very well for dimensional considerations. In particular, the math checks out: if $\omega$ is $k$-dimensional and $\eta$ is $\ell$-dimensional, they are represented respectively by $n-k$ and $n-\ell$-surfaces, whose intersection has dimension $(n-k)+(n-\ell)-n= n-(k+\ell)$, which corresponds, as desired, to a $k+\ell$-form.
- $\dl x \wedge \dl x = 0$: The calculation of such a wedge requires a bit of thought. At first glance, it would seem that $\dl x \wedge \dl x = \dl x$, because we are intersecting a collection of hyperplanes with themselves. However, the computation cannot be done in this way, because a hyperplane is not traverse to itself!
The way around that is actually to work with two distinct representations of $\dl x$. Indeed, suppose the first $\dl x$ is represented by the hyperplanes $x = 0, \varepsilon, 2\varepsilon, \dots$. Then, instead of representing the second $\dl x$ by the same collection of hyperplanes, represent it through $x = \frac12 \varepsilon, (1+\frac12) \varepsilon, (2+\frac12)\varepsilon, \dots$. Then, we have two collections of hyperplanes which never intersect. Therefore, their intersections are transverse: indeed, they are empty. (Yes, an empty intersection is a Good Intersection.) In conclusion, $\dl x \wedge \dl x = 0$, as it ought to. - $\omega \wedge \eta = (-1)^{k\ell} \eta \wedge \omega$: To talk about this property, we would need to go back to the issue of orientations. However, without getting into it, it is a priori obvious that $\omega \wedge \eta = \pm \eta \wedge \omega$, as the intersection of two surfaces does not depend on the order in which the intersection is taken. However, the sign issues arise upon consideration of the orientation of the intersection.
Unfortunately, the subject of orientation is too complex to be discussed in a mere bullet point, so the term $(-1)^{k\ell}$ must remain mysterious for the time being. - Associativity: Like in the previous bullet point, it is obvious that the wedge product would be associative up to sign. To show that the orientations of $\alpha \wedge (\beta \wedge \gamma)$ and $(\alpha \wedge \beta) \wedge \gamma$ match up would require a deeper inspection of the orientation conventions, but it does check out.
[Note to future self: Write another post discussing orientations in more detail?]
Exterior Derivative of a Wedge Product
The following picture should speak for itself, modulo orientations.
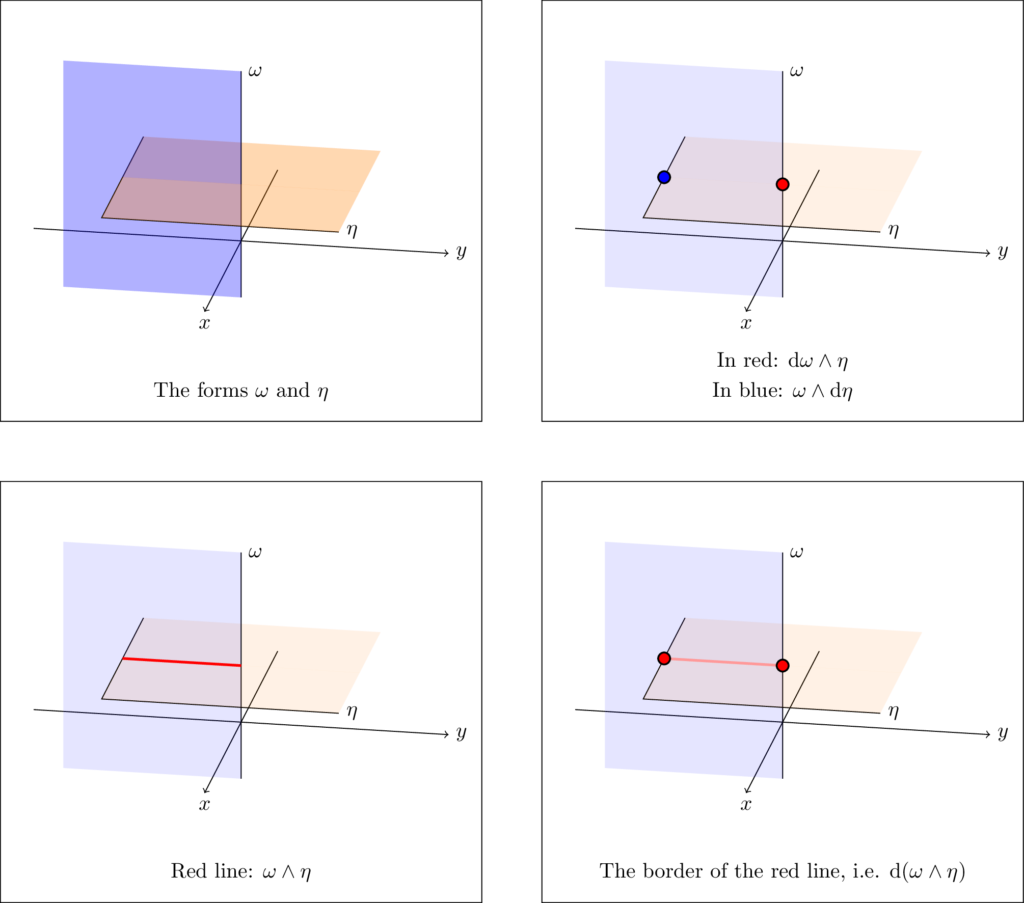
Again, to figure out the signs one would need a more careful look at orientations, which is beyond the scope of this post, but the formula is given by
\[\dl(\omega \wedge \eta) = \dl \omega \wedge \eta + (-1)^k \omega \wedge \dl \eta\text{, for $\omega$ of dimension $k$.}\]
Pullbacks and Lie Derivatives
Pullbacks
Let $M$ and $N$ be manifolds, and $f \colon M \to N$ a smooth function. Then, the pullback of a form $\omega$ on $N$ is usually defined as follows:
\[f^* \omega(v_1, \dots, v_k) := \omega((\dl f)v_1, \dots, (\dl f) v_k).\]
Symbolically, this is a very natural operation to define, but it also finds a nice interpretation in our framework.
For simplicity, let us consider a one-form $\omega$ on $N$, though the following argument applies to higher-dimensional forms as well. Recall that we represent $\omega$ through a collection of hypersurfaces, and to evaluate $\omega(v)$ on a vector $v$ tangent to $N$ we count how many of the hypersurfaces the vector $v$ crosses.
Consequently, to evaluate $f^* \omega$ on a vector $w$ tangent to $M$, what one does is push the vector $w$ forwards and counts how many surfaces of $\omega$ it crosses. However, a bit of mental gymnastics should convince you of the following alternative definition: To evaluate $f^*\omega(w)$, pull the surfaces composing $\omega$ back into $M$ (taking their preimage in $f$), and count how many of those $w$ crosses. In other words, we can represent $f^*\omega$ using the preimages of the surfaces that represent $\omega$.
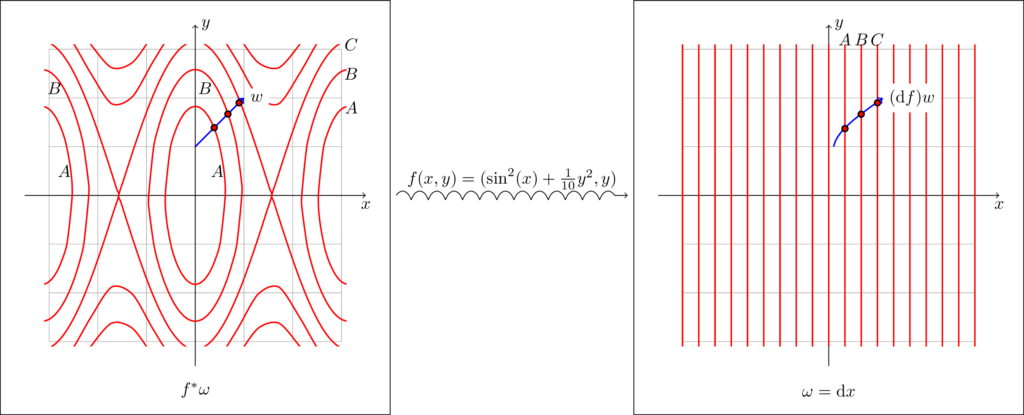
Like many others so far, this definition comes with a few of asterisks, because it is not obvious that taking the preimage under $f$ of the atoms of $\omega$ will yield a collection of atoms of the right dimension. Less obvious yet is that preimages behave well under borders, i.e. that $\partial f^{-1}(A) = f^{-1}(\partial A)$, where $A$ is one of the atoms of $\omega$ and $\partial$ is the border operator. I myself do not understand the underlying mechanics particularly well, though this post will be updated if this unfortunate state of affairs happens to change.
However, shady though it may seem, it appears to be the case that in general the border of the preimage coincides with the preimage of the border, and so we reach the classical fact:
\[ \dl(f^* \omega) = f^* (\dl \omega).\]
Lie Derivatives
First, let us recall the usual definition of Lie derivative.
Let $\omega$ be a form on $M$, and $X$ a vector field. Let $\phi_t$ be the time-$t$ flow of $X$. Of course, there are domain issues when considering flows, but we will sweep it all under the rug.
We define the Lie Derivative of $\omega$ in the direction of $X$ by the formula
\[\Lie_X \omega = \Eval{\doverd t}_0 \phi_t^* \omega.\]
In order to inspect this definition, let us begin by considering the pullback of a form by a flow. As we have seen, the pullback of a form can be visualized by taking the preimage of the form’s atoms, so we can visualize $\phi_t^* \omega$ by “flowing the atoms of $\omega$ backwards with $X$”.
This kind of moving visualization is harder to make drawings of, so I ask the reader to use their imagination to visualize the following example. Consider the form $\omega = \dl x \wedge \dl y$ in $\R^2$, visualized as a uniform grid of points. Let $X$ be the radial vector field $X_{(x,y)} = x \partial_x + y \partial_y$.
We will visualize $\phi_t^* \omega$ as $t$ varies by visualizing the motion of the atoms. Of course, for $t = 0$ there has been no motion, so we begin by seeing a uniform grid of points in $\R^2$.
Then, we begin flowing for positive time. The vector field in question points outwards from the origin, so since we are taking the preimage under the flow we move the atoms inwards. By solving the ODE, it is easy to check that an atom starting at $(x,y)$ will, after time $t$, be at the point $\e^{-t} (x, y)$. Therefore, we conclude that our uniform mesh of points is being pulled towards the origin in a way that preserves uniformity: after time $t$, distances between points have been uniformly compressed by a factor of $\e^{-t}$.
This even allows us to compute explicitly $\phi_t^* \omega$. Indeed, a uniform mesh of points represents a form of the type $C \dl x \wedge \dl y$, so all that remains is to find $C$. A heuristic argument is as follows: since in every direction, points are denser by a factor of $\e^{-t}$, the amount of points in a given parallelogram has been increased by $(\e^t)^2$. In other words, we claim that $\phi_t^* \omega = \e^{2t} \dl x \wedge \dl y$.
A slightly less heuristic argument is to start with the unit square at time $t = 0$, and flow it for time $t$. This will result in a smaller square, of side $\e^{-t}$, which contains exactly the same atoms, whence we conclude
\[\phi_t^* \omega (\e^{-t} \partial_x, \e^{-t} \partial_y) = \omega(\partial_x, \partial_y) = 1.\]
A few algebraic manipulations will yield again the result $C = \e^{2t}$.
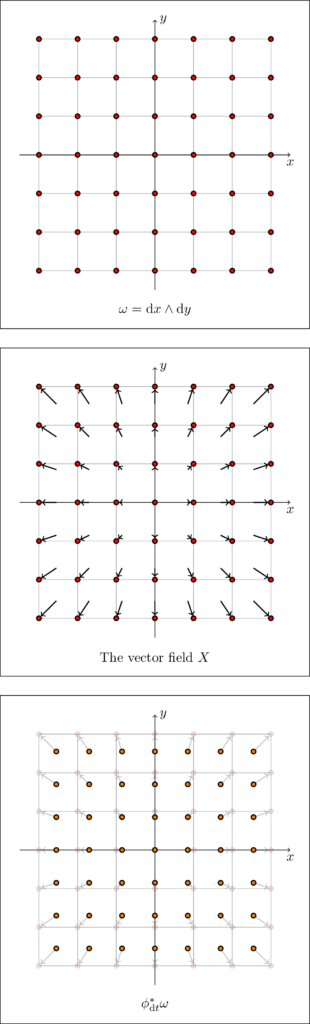
Now that we are familiar with the pullback of a form under a flow, all that remains is to differentiate. Unfortunately, the only visualization I am able to provide is very lackluster, and I encourage any reader who has a better idea to contact me.
Let us visualize differentiation using infinitesimals. In what follows, let $\dl t$ be a very small positive number. Then, $\Eval{\doverd t}_0 \phi_t^* \omega = \frac1{\dl t} (\phi_{\dl t}^* \omega – \omega)$. In other words, we begin by taking $\omega$, flowing it backwards through $X$ for infinitesimal time, and subtracting $\omega$ again. Now, this is zero to zeroth order, so we divide by $\dl t$ in order to get a real-valued thing.
Let’s elaborate a bit on the flow part for a moment. To first order, taking the flow in infinitesimal time is just calculating the velocity vector at the point and moving in the direction of the tip. In other words, (visualizing vectors as infinitesimal arrows) we may visualize $\phi_{\dl t}^* \omega$ by, for each point $p$ of each atom $A$, evaluating $X_p$ at that point and placing the arrow so that the tip is at $p$. Then, we replace $p$ by the tail of the arrow $X_p$. Doing this process for each point $p$, we obtain a new surface $B$, which is the atom of $\phi_{\dl t}^* \omega$ which corresponds to the atom $A$ in $\omega$. Repeating this process for every atom $A$ we obtain the atoms of $\phi_{\dl t}^* \omega$.
See the figure on the right for the example with the volume form $\omega$ on $\R^2$, and the radial field. Given a red atom at $(x,y)$, the corresponding orange atom is given by $(x,y)-\dl t X_{(x,y)}$, that is,
\[(x,y)-\dl t X_{(x,y)} = (1-\dl t)(x,y).\]
Therefore, we have a grid of uniformly spaced atoms, with a unit square with sides $(1-\dl t) \partial_x$ and $(1-\dl t) \partial_y$. Therefore, an argument similar to above will show that the orange atoms represent the form
\[\phi^*_{\dl t} \omega = (1-\dl t)^{-2} \dl x \wedge \dl y,\]
and therefore we may calculate the Lie derivative of $\omega$ in the direction of $X$:
\[\Lie_X \omega = \frac1{\dl t} (\phi_{\dl t}^* \omega – \omega) = \frac1{\dl t} ((1 – \dl t)^{-2} – 1) \dl x \wedge \dl y,\]
and a bit of elementary calculus shows that, taking the limit $\dl t \to 0$,
\[\Lie_X \omega = \frac{(1 – \dl t)^{-2} – 1}{\dl t} \dl x \wedge \dl y = 2 \dl x \wedge \dl y.\]
Contraction/Inner Product
At first, it seems difficult to visualize the contraction, because it is explicitly defined in terms of evaluation. In case you’ve forgotten or have never heard of it, given a $k$-form $\omega$ and a vector field $X$, we define the contraction $X \into \omega$ as
\[(X \into \omega)(v_1, \dots, v_{k-1}) := \omega(X, v_1, \dots, v_{k-1}).\]
To see an easy example of how such a form can be drawn, consider the simple example $M = \R^2$, $X = \partial_x$ and $\omega = \dl x \wedge \dl y$.
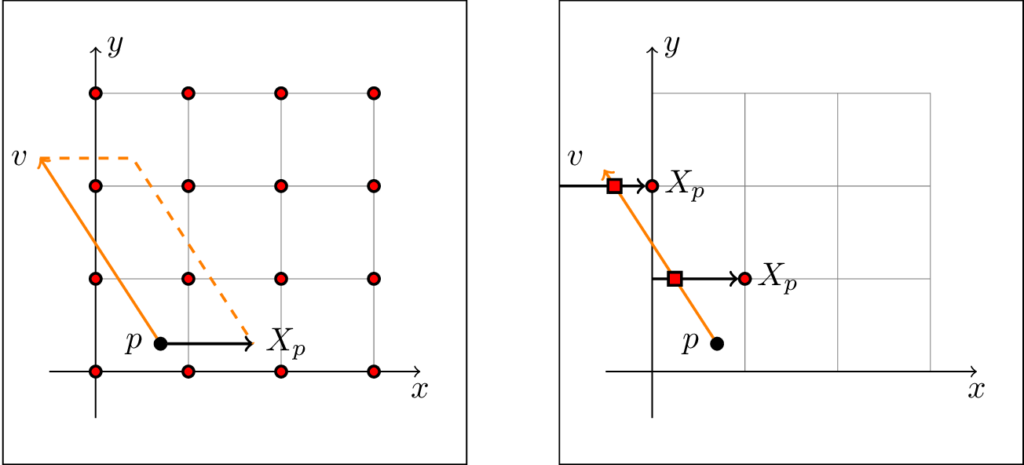
The idea, as seen in the image above, is to count the amount of atoms inside the parallelogram spanned by $v$ and $X$ by counting intersections. Indeed, roughly speaking, a point $q$ is inside the parallelogram spanned by $v$ and $X$ if and only if there exist $\alpha, \beta \in [0,1]$ such that
\[q = p + \alpha v + \beta X.\]
Rearranging terms, one concludes that this happens if and only if there exist such $\alpha$ and $\beta$ such that
\[p + \alpha v = q – \beta X,\]
that is, the line segment that goes from $p$ to $(p+v)$ intersects the line segment that goes from $(q-X)$ to $q$.
A simple calculation will yield a similar result for higher dimensions and for forms with non-point atoms. The general rule is as follows:
To represent $X \into \omega$ as a form, we construct its atoms out of the atoms of $\omega$ as follows. If $A$ is an atom of $\omega$, i.e. an $n-k$-manifold, at each of its points $a$ we calculate $X_a$, and draw this vector with the arrow tip on $A$. We then take the union of all the points on all of these vectors, yielding an $n-k+1$-manifold, which we call $X \into A$. The atoms of $X \into \omega$ are all those of the form $X \into A$.
Alternate definition of $X \into A$: The points of the form $a – t X_a$, for $a \in A$ and $t \in [0,1]$.
Let’s look at the example above again, and calculate $X \into \omega$. This case is particularly easy, but we will see that sometimes the visualization of $X \into \omega$ requires some mental gymnastics.
In this case, we begin by drawing a uniform grid of points, and drawing $X$ at each point. Then, we just consider the collection of resulting line segments.
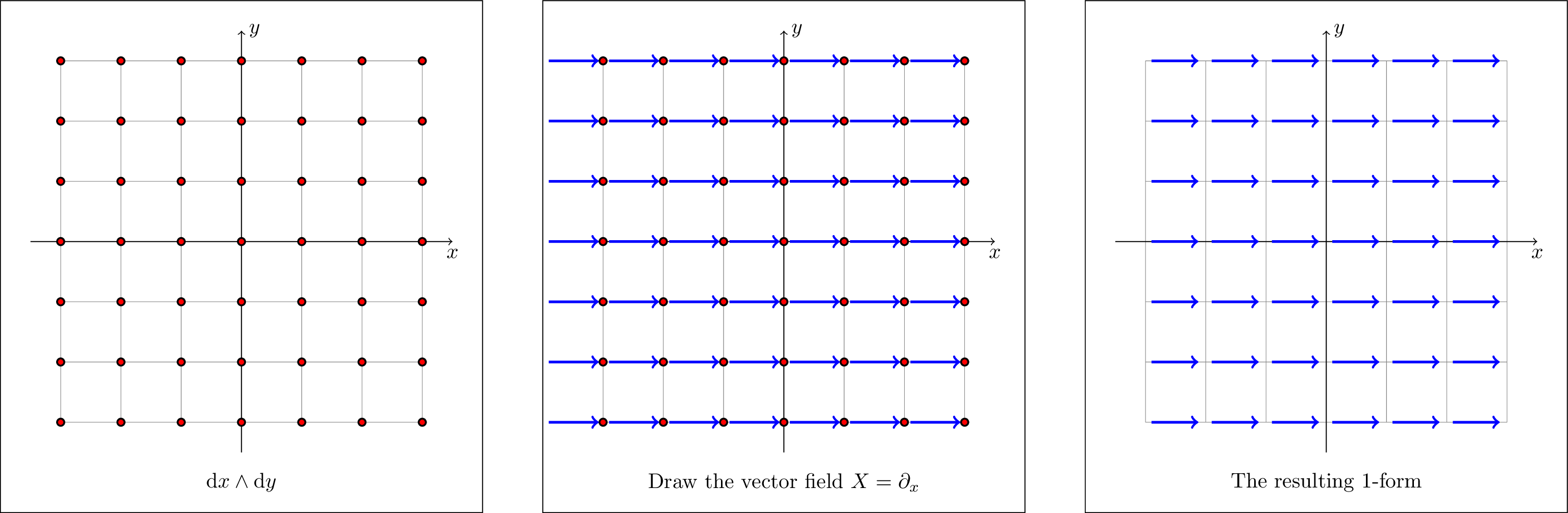
As you can see, this is a collection of line segments which are organized in rows, where each row is composed of infinitely many (length one) line segments. However, the way that the form is evaluated on a vector would not change if we glued these line segments together. So we glue them, and lo and behold, we get a uniform collection of horizontal lines, also known as $\dl y$, so we conclude
\[\partial_x \into (\dl x \wedge \dl y) = \dl y.\]
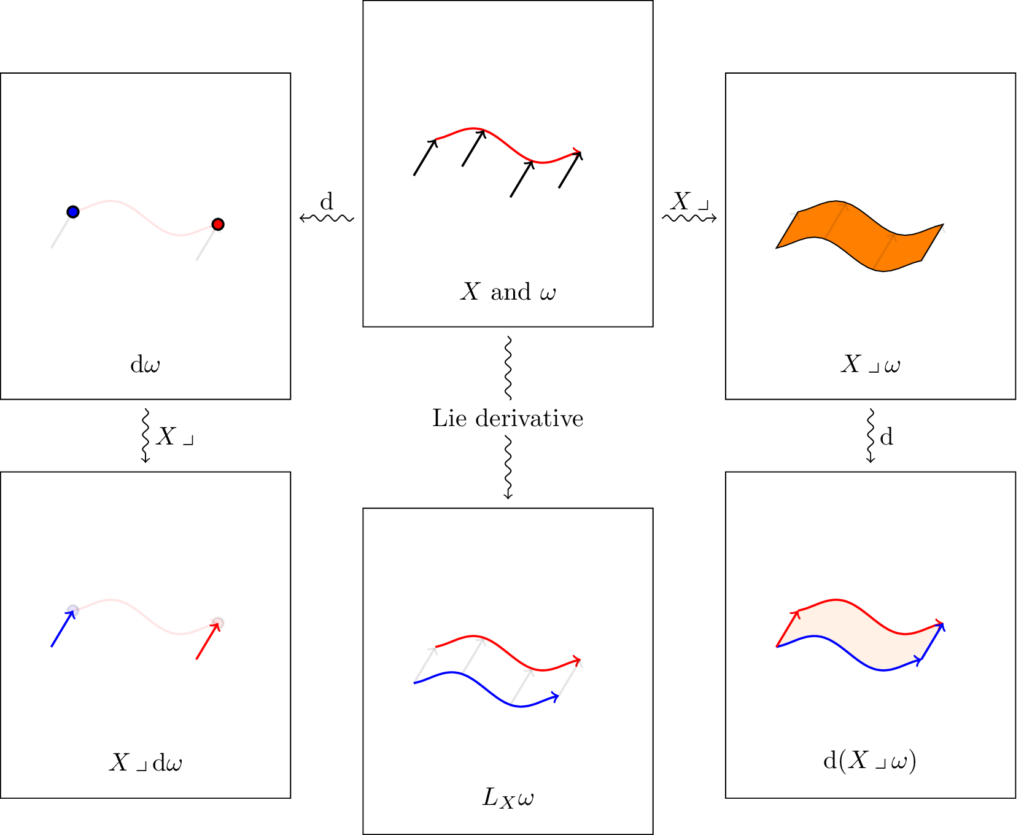
Cartan’s Magical Formula
We are now ready to look at Cartan’s magic formula for the Lie derivative, as we have already seen the three necessary ingredients: the Lie derivative, contraction, and the exterior derivative.
Let us begin by noting the relation between these three concepts. Given a vector field $X$ and a form $\omega$, both the Lie derivative and the contraction are related to the notion of “gluing the tip of $X$ into the atoms of $\omega$”. Indeed, if $\omega$ is a top form (i.e. its atoms are points) a useful identity appears:
\[\Lie_X \omega = \dl(X \into \omega).\]
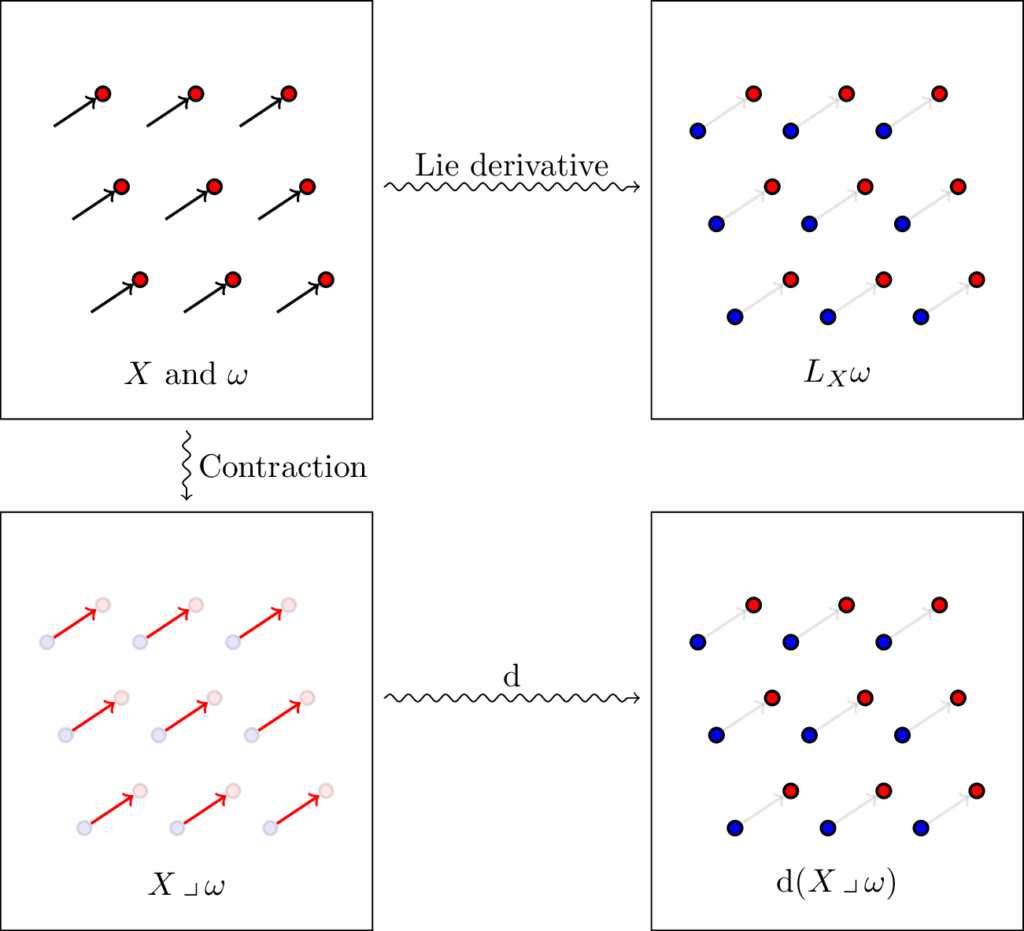
This identity is the first version of Cartan’s magic formula, and it actually works whenever $\omega$ is a closed form. However, when $\omega$ has atoms with nonempty border, a new term appears. To visualize why, suppose that $\omega$ is not a closed form, and has an atom $A$ with border $\partial A$. Assume for the sake of terminology that $A$ is one-dimensional, so that we may call it a curve with one or two extrema. Then, $X \into A$ is a strip. One of its sides is exactly $A$. Let us call the opposite side $B$, and the one or two other sides will be called $C$. Then, on the one hand, the atom corresponding to $\Lie_X \omega$ is simply $A+B$. On the other hand, $\dl(X \into \omega)$ includes $A$ and $B$, but also $C$, so we need to remove that term. A little bit of thought shows that $C$ is an atom from $X \into \dl \omega$, and so, modulo signs, we reach the famous formula
\[\Lie_X \omega = \dl(X \into \omega) + X \into \dl \omega.\]
This is amazingly helpful. Do you have a pdf verson of this.
Highly descriptive blog, I liked that a lot.
Will there be a part 2?
Wow, superb blog structure! How long have you been blogging for?
you made running a blog look easy. The full glance of your web
site is fantastic, as well as the content material! You can see similar here sklep
Wonderful website. A lot of useful info here. I am sending it to some buddies ans additionally sharing in delicious. And certainly, thanks for your sweat!
Simply desire to say your article is as astounding. The clarity in your post is just spectacular and i could assume you are an expert on this subject. Well with your permission let me to grab your feed to keep up to date with forthcoming post. Thanks a million and please keep up the gratifying work.
It’s really a great and helpful piece of info. I’m glad that you shared this helpful info with us. Please keep us up to date like this. Thanks for sharing.
It’s really a cool and helpful piece of information. I am glad that you shared this useful information with us. Please keep us up to date like this. Thank you for sharing.
Please let me know if you’re looking for a author for your site. You have some really great articles and I think I would be a good asset. If you ever want to take some of the load off, I’d really like to write some content for your blog in exchange for a link back to mine. Please shoot me an email if interested. Kudos!
You need to participate in a contest for the most effective blogs on the web. I’ll suggest this website!
Hello! I just would like to give a huge thumbs up for the great info you have here on this post. I will be coming back to your blog for more soon.
Howdy, i read your blog from time to time and i own a similar one and i was just wondering if you get a lot of spam remarks? If so how do you stop it, any plugin or anything you can recommend? I get so much lately it’s driving me crazy so any support is very much appreciated.
You made some first rate points there. I seemed on the web for the issue and found most individuals will go along with together with your website.
I¦ve been exploring for a little for any high-quality articles or weblog posts in this kind of house . Exploring in Yahoo I ultimately stumbled upon this site. Reading this information So i¦m happy to show that I have a very just right uncanny feeling I came upon exactly what I needed. I most for sure will make sure to do not omit this website and give it a look on a constant basis.
I like the efforts you have put in this, thank you for all the great posts.
After study a few of the blog posts on your website now, and I truly like your way of blogging. I bookmarked it to my bookmark website list and will be checking back soon. Pls check out my web site as well and let me know what you think.
Spot on with this write-up, I truly suppose this website needs rather more consideration. I’ll most likely be once more to read much more, thanks for that info.
You could definitely see your enthusiasm in the paintings you write. The sector hopes for more passionate writers such as you who aren’t afraid to mention how they believe. At all times follow your heart. “He never is alone that is accompanied with noble thoughts.” by Fletcher.
Hi! Someone in my Myspace group shared this site with us so I came to take a look. I’m definitely enjoying the information. I’m book-marking and will be tweeting this to my followers! Fantastic blog and outstanding design and style.
I see something really special in this website.
Hiya, I am really glad I have found this information. Today bloggers publish just about gossips and web and this is really irritating. A good website with interesting content, that is what I need. Thanks for keeping this web-site, I’ll be visiting it. Do you do newsletters? Can not find it.
Amazing! Its in fact remarkable article, I have got much clearidea on the topic of from this paragraph
Great post however I was wanting to know if you could write a litte more on this topic? I’d be very thankful if you could elaborate a little bit more. Bless you!
Throughout this awesome pattern of things you receive a B- just for effort and hard work. Where you actually misplaced everybody was in your specifics. As they say, details make or break the argument.. And that couldn’t be much more accurate here. Having said that, allow me say to you just what exactly did work. Your writing can be quite powerful which is probably the reason why I am making an effort in order to comment. I do not really make it a regular habit of doing that. 2nd, despite the fact that I can notice the leaps in reasoning you make, I am not certain of just how you appear to connect the ideas which inturn help to make your conclusion. For now I shall yield to your position but hope in the foreseeable future you actually connect your dots better.
I discovered your blog site on google and check a few of your early posts. Continue to keep up the very good operate. I just additional up your RSS feed to my MSN News Reader. Seeking forward to reading more from you later on!…
I have not checked in here for some time because I thought it was getting boring, but the last few posts are great quality so I guess I will add you back to my daily bloglist. You deserve it my friend 🙂
Yay google is my world beater aided me to find this great site! .
Hello, Neat post. There’s an issue together with your website in web explorer, may check this?K IE still is the marketplace leader and a big element of other folks will miss your great writing due to this problem.
Wow! Thank you! I permanently wanted to write on my site something like that. Can I include a fragment of your post to my blog?
Whats Taking place i’m new to this, I stumbled upon this I’ve found It positively helpful and it has helped me out loads. I’m hoping to contribute & assist other customers like its helped me. Good job.
Hello! Someone in my Myspace group shared this website with us so I came to give it a look. I’m definitely loving the information. I’m book-marking and will be tweeting this to my followers! Superb blog and wonderful design and style.
you have a great blog here! would you like to make some invite posts on my blog?
WONDERFUL Post.thanks for share..more wait .. …
Thanks for sharing superb informations. Your web-site is so cool. I am impressed by the details that you have on this blog. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for extra articles. You, my pal, ROCK! I found just the info I already searched everywhere and just could not come across. What an ideal website.
Great blog! I am loving it!! Will come back again. I am bookmarking your feeds also
Thanks for this post, I am a big fan of this website would like to continue updated.
Купить металлопрокат можно оптом и в розницу. Доставка по всей России от 2 дней. Металлопродукция: Трубы ВГП и Стальные, Лист горячекатаный, лист нержавеющий.
Thanks for another wonderful article. Where else could anybody get that type of info in such a perfect way of writing? I’ve a presentation next week, and I am on the look for such information.
hey there and thank you to your information – I’ve definitely picked up something new from right here. I did alternatively experience several technical points the usage of this website, as I experienced to reload the web site many occasions prior to I could get it to load properly. I have been brooding about in case your web host is OK? Not that I’m complaining, however slow loading cases instances will sometimes impact your placement in google and can harm your high-quality score if ads and ***********|advertising|advertising|advertising and *********** with Adwords. Well I’m adding this RSS to my email and could look out for much extra of your respective exciting content. Make sure you update this again very soon..
What i do not understood is in reality how you are not really a lot more neatly-preferred than you may be now. You are so intelligent. You understand thus considerably on the subject of this subject, produced me for my part imagine it from numerous various angles. Its like women and men are not interested until it is one thing to do with Lady gaga! Your personal stuffs great. All the time deal with it up!
I visited a lot of website but I think this one contains something extra in it in it
superb post.Ne’er knew this, appreciate it for letting me know.
hey there and thanks in your information – I have definitely picked up anything new from proper here. I did however experience some technical issues the usage of this website, as I skilled to reload the site many occasions prior to I may get it to load correctly. I have been brooding about in case your hosting is OK? Now not that I am complaining, however sluggish loading circumstances occasions will sometimes affect your placement in google and can injury your high quality rating if advertising and ***********|advertising|advertising|advertising and *********** with Adwords. Well I am including this RSS to my e-mail and could glance out for much extra of your respective fascinating content. Make sure you update this once more soon..
This is the right blog for anyone who wants to find out about this topic. You realize so much its almost hard to argue with you (not that I actually would want…HaHa). You definitely put a new spin on a topic thats been written about for years. Great stuff, just great!
Loving the info on this internet site, you have done outstanding job on the blog posts.
You could definitely see your expertise within the work you write. The sector hopes for even more passionate writers such as you who are not afraid to mention how they believe. Always go after your heart. “A second wife is hateful to the children of the first a viper is not more hateful.” by Euripides.
I got what you intend, regards for putting up.Woh I am pleased to find this website through google. “Success is dependent on effort.” by Sophocles.
Respect to op, some great selective information.
Hi my loved one! I want to say that this post is amazing, nice written and include almost all vital infos. I’d like to peer extra posts like this .
Howdy very nice website!! Guy .. Excellent .. Amazing .. I’ll bookmark your site and take the feeds also?KI am happy to find numerous useful information here within the submit, we need work out extra techniques in this regard, thank you for sharing. . . . . .
Great post and right to the point. I am not sure if this is actually the best place to ask but do you folks have any thoughts on where to get some professional writers? Thanks in advance 🙂
Wow! Thank you! I continuously wanted to write on my website something like that. Can I include a portion of your post to my blog?
I regard something really special in this web site.
Good write-up, I?¦m normal visitor of one?¦s blog, maintain up the nice operate, and It is going to be a regular visitor for a long time.
Some truly nice and utilitarian information on this internet site, too I think the style and design contains excellent features.
Excellent site. Lots of useful information here. I am sending it to some pals ans additionally sharing in delicious. And obviously, thanks in your sweat!
Excellent read, I just passed this onto a colleague who was doing some research on that. And he just bought me lunch because I found it for him smile So let me rephrase that: Thanks for lunch! “For most of history, Anonymous was a woman.” by Virginia Woolf.
I was suggested this website by my cousin. I’m not sure whether this post is written by him as nobody else know such detailed about my trouble. You are incredible! Thanks!
I’m impressed, I must say. Actually rarely do I encounter a weblog that’s each educative and entertaining, and let me let you know, you have hit the nail on the head. Your thought is outstanding; the difficulty is something that not enough individuals are talking intelligently about. I’m very completely happy that I stumbled across this in my seek for something regarding this.
of course like your web-site however you need to check the spelling on several of your posts. A number of them are rife with spelling problems and I in finding it very bothersome to tell the truth then again I’ll certainly come again again.
I do agree with all of the ideas you have presented in your post. They are very convincing and will definitely work. Still, the posts are too short for beginners. Could you please extend them a bit from next time? Thanks for the post.
Thank you for sharing superb informations. Your web-site is very cool. I’m impressed by the details that you have on this web site. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for more articles. You, my pal, ROCK! I found simply the information I already searched everywhere and just couldn’t come across. What a perfect web site.
My husband and i have been now thrilled when Chris could do his web research through the ideas he obtained using your weblog. It is now and again perplexing just to choose to be giving away guides that many others have been making money from. And now we discover we have got the website owner to be grateful to for this. The most important illustrations you have made, the straightforward site navigation, the friendships your site assist to foster – it is all awesome, and it’s leading our son in addition to our family know that that situation is fun, which is quite fundamental. Many thanks for all the pieces!
Greetings! Very helpful advice on this article! It is the little changes that make the biggest changes. Thanks a lot for sharing!
I like this weblog so much, saved to favorites.
Hello there, just became aware of your blog through Google, and found that it is really informative. I am going to watch out for brussels. I will appreciate if you continue this in future. A lot of people will be benefited from your writing. Cheers!
Thank you for any other informative blog. The place else could I get that type of information written in such a perfect way? I have a mission that I am simply now operating on, and I’ve been at the look out for such info.
It is perfect time to make some plans for the future and it’s time to be happy. I have read this post and if I could I want to suggest you some interesting things or advice. Maybe you could write next articles referring to this article. I want to read even more things about it!
Awesome website you have here but I was curious about if you knew of any forums that cover the same topics talked about in this article? I’d really like to be a part of online community where I can get responses from other experienced people that share the same interest. If you have any recommendations, please let me know. Thank you!
I am impressed with this web site, rattling I am a big fan .
I’ve read a few good stuff here. Definitely worth bookmarking for revisiting. I wonder how much effort you put to create such a great informative site.
Bursa escort bayan ve görükle escort profilleri ve iletişim bilgileri
Pretty! This was a really wonderful post. Thank you for your provided information.
Very interesting topic, thankyou for putting up.
bursa escort
引流
非小号官网
Very interesting info!Perfect just what I was looking for!
Woah! I’m really digging the template/theme of this blog. It’s simple, yet effective. A lot of times it’s hard to get that “perfect balance” between superb usability and visual appeal. I must say you have done a amazing job with this. Additionally, the blog loads extremely quick for me on Firefox. Exceptional Blog!
I have been reading out a few of your articles and i can state pretty clever stuff. I will surely bookmark your website.
I like this blog very much, Its a very nice berth to read and find information.
Cenforce 200 tablets significantly improve Erectile Dysfunction in men. It stands out as one of the most effective ED medications available today. Cenforce 200 is recommended for patients experiencing difficulties in maintaining a firm erection, even after trying various treatments. This medication is designed to enhance blood flow to the penis, ensuring a sustained erection.
Visit Now: >>> https://meds4go.com/cenforce-200/
Wow, incredible blog layout! How long have you been blogging for? you made blogging look easy. The overall look of your website is great, let alone the content!
I must point out my respect for your generosity giving support to individuals that really need guidance on this particular area of interest. Your very own commitment to passing the message all around had become remarkably effective and have permitted individuals just like me to arrive at their aims. Your new helpful help signifies a great deal to me and still more to my fellow workers. Best wishes; from everyone of us.
Hello, you used to write fantastic, but the last several posts have been kinda boring… I miss your tremendous writings. Past several posts are just a little out of track! come on!
Hmm is anyone else encountering problems with the images on this blog loading? I’m trying to determine if its a problem on my end or if it’s the blog. Any suggestions would be greatly appreciated.
快连VPN 采用全新内核，AI 智能连接，自动为您匹配全球最快的网络节点，只需要轻点“开启快连”，3秒之内，纵享丝绸般顺滑的冲浪体验。
AICoin offers you real-time global cryptocurrency market quotes, professional candlestick charts, outstanding Web3 data analysis, AI-powered data analytics, curated industry news, and an investor community for exchange. Experience a diversified and convenient one-stop service. Compatible with macOS, Windows, iOS, and Android devices.
aicoin下载ios
Thankyou for all your efforts that you have put in this. very interesting information.
Wow! This can be one particular of the most helpful blogs We’ve ever arrive across on this subject. Actually Great. I’m also a specialist in this topic therefore I can understand your hard work.
Are you struggling to improve your website’s ranking on Google? Do you want to enhance your online presence and drive more organic traffic to your site? Look no further! I offer a premium service to help you achieve top Google rankings with high-quality SEO backlinks.🌟 High-Quality Backlinks: I will provide you with powerful, high-authority backlinks from reputable sources to significantly boost your website’s ranking on Google.
Are you struggling to improve your website’s ranking on Google? Do you want to enhance your online presence and drive more organic traffic to your site? Look no further! I offer a premium service to help you achieve top Google rankings with high-quality SEO backlinks.🌟 High-Quality Backlinks: I will provide you with powerful, high-authority backlinks from reputable sources to significantly boost your website’s ranking on Google.
Hello, i think that i saw you visited my site thus i came to “return the prefer”.I am trying to in finding issues to enhance my site!I suppose its ok to use a few of your concepts!!
Wohh exactly what I was searching for, appreciate it for putting up.
Are you struggling to improve your website’s ranking on Google? Do you want to enhance your online presence and drive more organic traffic to your site? Look no further! I offer a premium service to help you achieve top Google rankings with high-quality SEO backlinks.🌟 High-Quality Backlinks: I will provide you with powerful, high-authority backlinks from reputable sources to significantly boost your website’s ranking on Google.
Elevate your sniping capabilities with Flash Bot, delivering unmatched efficiency across over 40 networks, including Ethereum, BSC, and Solana.
Good website! I really love how it is easy on my eyes and the data are well written. I’m wondering how I could be notified whenever a new post has been made. I’ve subscribed to your RSS which must do the trick! Have a great day!
Thanks for the sensible critique. Me & my neighbor were just preparing to do some research on this. We got a grab a book from our local library but I think I learned more clear from this post. I’m very glad to see such excellent information being shared freely out there.
I love it when people come together and share opinions, great blog, keep it up.
My partner and I absolutely love your blog and find most of your post’s to be precisely what I’m looking for. Does one offer guest writers to write content to suit your needs? I wouldn’t mind producing a post or elaborating on a number of the subjects you write regarding here. Again, awesome blog!
Very interesting subject , thanks for posting.
Explore all Fryd carts flavors, including new and disposable options. Buy now for the ultimate vaping experience. Satisfaction guaranteed!
Explore all Fryd carts flavors, including new and disposable options. Buy now for the ultimate vaping experience. Satisfaction guaranteed!
I like what you guys are up too. Such smart work and reporting! Keep up the superb works guys I have incorporated you guys to my blogroll. I think it will improve the value of my site :).
Those are yours alright! . We at least need to get these people stealing images to start blogging! They probably just did a image search and grabbed them. They look good though!
Undeniably believe that which you stated. Your favorite reason appeared to be on the internet the easiest thing to be aware of. I say to you, I certainly get irked while people consider worries that they plainly do not know about. You managed to hit the nail upon the top and defined out the whole thing without having side-effects , people can take a signal. Will likely be back to get more. Thanks
After study a few of the blog posts on your website now, and I truly like your way of blogging. I bookmarked it to my bookmark website list and will be checking back soon. Pls check out my web site as well and let me know what you think.
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point. You definitely know what youre talking about, why waste your intelligence on just posting videos to your site when you could be giving us something enlightening to read?
I have recently started a website, the info you provide on this site has helped me tremendously. Thanks for all of your time & work.
I like this web blog very much, Its a very nice position to read and get info . “A fair exterior is a silent recommendation.” by Publilius Syrus.
HEMA4D adalah Situs Slot Online Server Pay4d Tergacor dan Terpercaya hari ini 2024 dengan tingkat kemenangan tertinggi dan memiliki provider game slot tergacor gampang menang hari ini
It is in point of fact a great and useful piece of information. I am satisfied that you just shared this useful information with us. Please keep us informed like this. Thanks for sharing.
Thank you for helping out, great info. “The health of nations is more important than the wealth of nations.” by Will Durant.
78win mang den lan gio giai tri moi la khac biet khien cong dong nguoi choi thich thu lien tuc truyen tai nhau. Nha cai hoat dong hop phap uy tin hang dau chau A voi cac dich vu dang cap chuyen nghiep. Noi day chinh la diem dung chan dich thuc cua cac cuoc thu me game do den.https://78win.kids/
That is the suitable weblog for anyone who needs to search out out about this topic. You realize a lot its nearly laborious to argue with you (not that I actually would want…HaHa). You positively put a new spin on a topic thats been written about for years. Nice stuff, simply great!
I’m still learning from you, as I’m improving myself. I definitely love reading all that is posted on your blog.Keep the stories coming. I enjoyed it!
Really clean web site, appreciate it for this post.
Hi, i think that i saw you visited my website so i came to “return the favor”I’m trying to find things to enhance my website!I suppose its ok to use a few of your ideas!!
Thanks for another excellent post. Where else could anybody get that type of info in such an ideal way of writing? I’ve a presentation next week, and I am on the look for such information.
Thanks for any other informative website. The place else may just I am getting that type of info written in such a perfect method? I have a project that I’m just now operating on, and I’ve been on the glance out for such info.
Can I simply say what a aid to search out someone who truly knows what theyre speaking about on the internet. You definitely know how one can convey an issue to mild and make it important. Extra folks must learn this and perceive this aspect of the story. I cant consider youre no more widespread because you undoubtedly have the gift.
You have brought up a very superb details, regards for the post.
Simply desire to say your article is as surprising. The clearness to your post is simply nice and that i could suppose you are knowledgeable in this subject. Well with your permission allow me to clutch your feed to keep updated with approaching post. Thanks a million and please keep up the gratifying work.
Saved as a favorite, I really like your blog!
Excellent blog here! Also your website so much up fast! What web host are you the usage of? Can I am getting your associate link to your host? I desire my website loaded up as quickly as yours lol
I haven?¦t checked in here for some time since I thought it was getting boring, but the last few posts are great quality so I guess I will add you back to my daily bloglist. You deserve it my friend 🙂
Hello my friend! I wish to say that this article is amazing, great written and include approximately all significant infos. I would like to look extra posts like this .
Greetings! Very helpful advice on this article! It is the little changes that make the biggest changes. Thanks a lot for sharing!
I conceive you have mentioned some very interesting details , thankyou for the post.
You have mentioned very interesting details! ps nice web site. “I understand a fury in your words, But not the words.” by William Shakespeare.
I love what you guys are up too. This type of clever work and exposure! Keep up the fantastic works guys I’ve incorporated you guys to my blogroll.
Throughout this grand design of things you actually receive a B+ for effort. Exactly where you confused me ended up being in all the specifics. You know, they say, the devil is in the details… And that couldn’t be much more true here. Having said that, let me tell you just what exactly did do the job. The authoring is really persuasive and this is possibly the reason why I am taking the effort in order to comment. I do not really make it a regular habit of doing that. 2nd, despite the fact that I can see a jumps in reasoning you come up with, I am not really certain of how you seem to unite your details which in turn make your final result. For now I will, no doubt subscribe to your position but hope in the near future you actually connect your dots much better.
Wow! Thank you! I always needed to write on my website something like that. Can I implement a portion of your post to my blog?
Your house is valueble for me. Thanks!…
I really appreciate this post. I’ve been looking everywhere for this! Thank goodness I found it on Bing. You have made my day! Thank you again!
Khá nhiều anh em chọn SOC88 để tái tạo năng lượng, có thêm sự sảng khoái. Sân chơi đẳng cấp này còn mở ra cơ hội để bạn sớm thắng đậm.Chính những ưu việt sau giúp địa chỉ cá cược trực tuyến kể trên được nhiều người tìm tới. Tin rằng, những trải nghiệm của bạn tại đây cũng rất giá trị đấy! . https://tipsthuthuat.com/
I really like examining and I believe this website got some truly utilitarian stuff on it! .
I truly appreciate this post. I?¦ve been looking all over for this! Thank goodness I found it on Bing. You have made my day! Thank you again
Some really interesting information, well written and loosely user friendly.
I enjoy your piece of work, thanks for all the good posts.
I’d have to examine with you here. Which is not one thing I usually do! I take pleasure in reading a post that may make folks think. Additionally, thanks for permitting me to comment!
It is in point of fact a great and useful piece of info. I am satisfied that you just shared this useful info with us. Please keep us informed like this. Thanks for sharing.
Awsome info and right to the point. I am not sure if this is truly the best place to ask but do you folks have any thoughts on where to hire some professional writers? Thank you 🙂
The Grand Goldman online store curates an extensive collection of premium travel gifts sourced from diverse cultures worldwide. This platform goes beyond mere product offerings, serving as a comprehensive resource for globetrotters, couples, and families alike. It features carefully selected, unique items that capture the essence of international destinations, complemented by expert recommendations and inspiring travel ideas. Grand Goldman’s thoughtfully curated inventory caters to discerning travelers and gift-givers, offering both practical essentials and decorative pieces that reflect the richness of global heritage.
The other day, while I was at work, my cousin stole my iphone and tested to see if it can survive a thirty foot drop, just so she can be a youtube sensation. My iPad is now broken and she has 83 views. I know this is entirely off topic but I had to share it with someone!
I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
Some truly great info , Sword lily I noticed this. “It’s not only the most difficult thing to know one’s self, but the most inconvenient.” by Josh Billings.
I was reading through some of your articles on this site and I conceive this site is very informative! Keep on posting.
ProNerve 6 nerve relief formula stands out due to its advanced formula combining natural ingredients that have been specifically put together for the exceptional health advantages it offers.
Its like you read my mind! You seem to know a lot about this, like you wrote the book in it or something. I think that you can do with some pics to drive the message home a bit, but other than that, this is fantastic blog. A great read. I will certainly be back.
VN88 da xuat hien va phat trien tren thi truong ca cuoc tu nam 2019 den nay, tich luy duoc gan 4 nam kinh nghiem hoat dong. Tu ngay khi ra mat, VN88 da nhan duoc su danh gia cao va su ua chuong cua dong dao nguoi choi, chinh nho chat luong hang dau vao nam 2023 https://vn88-vn.com/
Ww88 la trang dai ly chinh thuc, chuyen cung cap link dang nhap vao nha cai W88 chinh xac nhat ma ban khong phai lo truy cap phai trang gia mao.
Noi ve nha cai W88 co le khong dan me bong da nao lai khong thay mot lan cac doi bong ngoai hang anh mac ao do cong ty nay tai tro. https://ww88-vn.com/
Nice read, I just passed this onto a colleague who was doing some research on that. And he actually bought me lunch since I found it for him smile Therefore let me rephrase that: Thanks for lunch!
You completed certain nice points there. I did a search on the subject and found a good number of persons will consent with your blog.
Heya i’m for the first time here. I came across this board and I find It truly useful & it helped me out much. I hope to give something back and help others like you helped me.
F*ckin’ awesome things here. I am very glad to see your post. Thanks a lot and i’m looking forward to contact you. Will you please drop me a mail?
Tim ngay link vao nha cai SOC88 khong bi chan de tranh website gia mao. Anh em som co the tiep can cac game hay tai dia chi ca cuoc truc tuyen uy tin hang dau Viet Nam nay. https://soc88b.vip/
Hi! I’m SEO QUEEN. I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
Hi! I’m SEO QUEEN. I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
Hi! I’m SEO QUEEN. I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
I like this web blog so much, saved to bookmarks. “I don’t care what is written about me so long as it isn’t true.” by Dorothy Parker.
I?¦ve read some excellent stuff here. Certainly worth bookmarking for revisiting. I surprise how much attempt you place to create one of these fantastic informative website.
Hi! I’m SEO QUEEN. I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
It’s really a nice and useful piece of information. I am glad that you shared this useful info with us. Please keep us up to date like this. Thanks for sharing.
Im not certain the place you are getting your information, but good topic. I must spend some time learning much more or understanding more. Thank you for fantastic info I was searching for this information for my mission.
I got what you mean ,saved to bookmarks, very nice site.
Cổng game Go88 đã mua lại tên miền https://pacoveredbridges.com/ và sử dụng tên miền mới này để phát hành game tại thị trường Việt Nam.
Kuailian Game Accelerator helps overseas Chinese accelerate global mainstream and domestic games, as well as mainstream domestic applications, and enjoy the acceleration of global audio and video resources. One-click direct connection, permanently free, watch videos, live broadcasts, listen to music, and play domestic games anytime, anywhere.
You are a very bright person!
Kuailian Game Accelerator helps overseas Chinese accelerate global mainstream and domestic games, as well as mainstream domestic applications, and enjoy the acceleration of global audio and video resources. One-click direct connection, permanently free, watch videos, live broadcasts, listen to music, and play domestic games anytime, anywhere.
Kuailian Game Accelerator helps overseas Chinese accelerate global mainstream and domestic games, as well as mainstream domestic applications, and enjoy the acceleration of global audio and video resources. One-click direct connection, permanently free, watch videos, live broadcasts, listen to music, and play domestic games anytime, anywhere.
Kuailian Game Accelerator helps overseas Chinese accelerate global mainstream and domestic games, as well as mainstream domestic applications, and enjoy the acceleration of global audio and video resources. One-click direct connection, permanently free, watch videos, live broadcasts, listen to music, and play domestic games anytime, anywhere.
Hello, Neat post. There is a problem together with your website in web explorer, may check thisK IE still is the marketplace chief and a good component to other people will omit your magnificent writing because of this problem.
快连VPN以用户友好著称。该应用程序具有简洁直观的界面，使各种技术水平的用户都能轻松导航和使用。只需几次点击，您就可以连接到安全服务器并开始安全浏览。
I conceive this site has got some very good info for everyone. “The foundation of every state is the education of its youth.” by Diogenes.
Undeniably believe that which you stated Your favorite reason appeared to beon the net the simplest thing to be aware of I say to you, I definitely get irked while people consider worriesthat they plainly do not know about You managed to hitthe nail upon the top as well as defined out the whole thing without having side effect , people could take a signalWill likely be back to get more Thanks
There are some fascinating cut-off dates in this article however I don’t know if I see all of them heart to heart. There’s some validity but I will take hold opinion till I look into it further. Good article , thanks and we wish more! Added to FeedBurner as properly
I keep listening to the newscast lecture about receiving free online grant applications so I have been looking around for the finest site to get one. Could you advise me please, where could i acquire some?
Nhà cái 888B được thành lập từ năm 2015 và đã hoạt động gần một thập kỷ trong lĩnh vực giải trí châu Á. Với nhiều thành tựu đáng chú ý và đội ngũ phát triển đã xây dựng nên một thương hiệu uy tín, được đại đa số người chơi tin cậy. 888B cam kết mang đến một môi trường minh bạch, an toàn và công bằng nhất.
Wedsite: https://888b-vn.com/
Lovely just what I was searching for.Thanks to the author for taking his time on this one.
Website Analysis: I will analyze your website and keyword landscape to formulate a customized backlink strategy.
As soon as I detected this web site I went on reddit to share some of the love with them.
I am not really great with English but I come up this real leisurely to understand.
I have learn a few just right stuff here. Definitely worth bookmarking for revisiting. I surprise how much attempt you put to create the sort of great informative web site.
I loved as much as you’ll receive carried out right here. The sketch is attractive, your authored material stylish. nonetheless, you command get got an impatience over that you wish be delivering the following. unwell unquestionably come further formerly again as exactly the same nearly a lot often inside case you shield this hike.
I enjoy your writing style really enjoying this web site.
Very wonderful info can be found on blog.
The next time I read a blog, I hope that it doesnt disappoint me as much as this one. I mean, I know it was my choice to read, but I actually thought youd have something interesting to say. All I hear is a bunch of whining about something that you could fix if you werent too busy looking for attention.
Your style is so unique compared to many other people. Thank you for publishing when you have the opportunity,Guess I will just make this bookmarked.2
Rattling informative and good structure of subject material, now that’s user genial (:.
Great write-up, I am normal visitor of one’s blog, maintain up the nice operate, and It is going to be a regular visitor for a lengthy time.
When I initially commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get four e-mails with the same comment. Is there any way you can remove me from that service? Thanks!
Appreciate it for all your efforts that you have put in this. very interesting information.
Hi , I do believe this is an excellent blog. I stumbled upon it on Yahoo , i will come back once again. Money and freedom is the best way to change, may you be rich and help other people.
Very well written post. It will be valuable to anybody who utilizes it, as well as myself. Keep up the good work – i will definitely read more posts.
Thanks , I have recently been looking for info about this subject for ages and yours is the greatest I have discovered till now. But, what about the bottom line? Are you sure about the source?
Very well written post. It will be beneficial to anyone who utilizes it, including myself. Keep doing what you are doing – i will definitely read more posts.
I really appreciate this post. I¦ve been looking all over for this! Thank goodness I found it on Bing. You have made my day! Thx again
Neat blog! Is your theme custom made or did you download it from somewhere? A design like yours with a few simple tweeks would really make my blog shine. Please let me know where you got your design. Kudos
Merely wanna remark that you have a very decent site, I love the layout it really stands out.
Hey very cool web site!! Man .. Beautiful .. Amazing .. I’ll bookmark your site and take the feeds also…I’m happy to find a lot of useful information here in the post, we need work out more techniques in this regard, thanks for sharing. . . . . .
WONDERFUL Post.thanks for share..more wait .. …
789 win la mot trong nhung thuong hieu nha cai duoc gioi cuoc thu san don nhieu nhat hien nay. Danh gia cua nguoi choi sau khi trai nghiem thuc te tai nha cai nay vo cung tich cuc, gop phan lan truyen danh tieng cua 789WIN trong gioi ca cuoc https://789win-vn.com/
Nha cai Wi88 la san choi game ca cuoc the thao uy tin hang dau moi ra mat nam 2024 tai thi truong Viet Nam cung nhu chau A. La thuong hieu moi cua nha cai W88 noi tieng hon 30 nam, Wi88 cung so huu giao dien bat mat va keo cuoc da dang, thu hut dong dao cuoc thu tham gia moi ngay. Website : http://wi88.soccer/
I precisely desired to thank you very much once again. I’m not certain the things that I might have worked on in the absence of the type of thoughts revealed by you relating to my area. It absolutely was a real traumatic circumstance for me, nevertheless finding out the very specialized fashion you treated it forced me to jump with contentment. I am just grateful for the service and in addition sincerely hope you find out what an amazing job you’re getting into training most people by way of your web page. I’m certain you haven’t encountered all of us.
Hi, i read your blog from time to time and i own a similar one and i was just wondering if you get a lot of spam feedback? If so how do you prevent it, any plugin or anything you can advise? I get so much lately it’s driving me mad so any support is very much appreciated.
IPTV Smarters Pro has 17000+ Live Channels No Buffering content with 99 Uptime. trial available, +80k Movies & Series +20Gbps servers.
Excellent read, I just passed this onto a friend who was doing a little research on that. And he actually bought me lunch since I found it for him smile So let me rephrase that: Thanks for lunch!
I am not rattling good with English but I line up this very leisurely to understand.
I would like to thnkx for the efforts you have put in writing this blog. I am hoping the same high-grade blog post from you in the upcoming as well. In fact your creative writing abilities has inspired me to get my own blog now. Really the blogging is spreading its wings quickly. Your write up is a good example of it.
Respect to post author, some good entropy.
Saved as a favorite, I really like your blog!
Bermain Togel Online dengan 63 Pasaran WLA, tentu akan menghadirkan keseruan tersendiri, dimana setiap pecinta Togel Online dapat menikmati taruhan Togel selama 24 Jam tanpa batas. Ditambah dengan minimal deposit Rp 10.000 dan minimal betting Rp 100 perak yang rendah, maka bermain Togel Online akan semakin menarik dan mudah. Kami Bandar Petirjitu juga memnyediakan kemudahan dalam hal melakukan pengisian Deposit, dimana member dapat melakukan pengisian Deposit melalui Transfer Bank dan E-wallet seperti Ovo, Dana, Gopay & Link Aja.
فيب الرياض متجر مهتم بجميع منتجيات الشيشة الالكترونية والشيشة التقليدية معسلات تقليدية ومعسل الكتروني خيارات متنوعة بافضل الاسعار واسرع توصيل
لانجرينا يقدم تشكيلة واسعة من اللانجري والملابس الداخلية النسائية المثيرة والأنيقة. اكتشفي أجمل التصاميم والراحة المثالية لتجعلي كل لحظة خاصة.
متجر لبيع الفيب بالسعودية مختص يالمنتجات التي تستخدم في تدخين السجائر الإلكترونية. يوفر المتجر الأجهزة والنكهات والسوائل التي تستخدم في تعبئة السجائر الإلكترونية.
Throughout this great pattern of things you actually secure a B+ for effort. Where you actually misplaced us ended up being on all the facts. As it is said, the devil is in the details… And it could not be more accurate in this article. Having said that, allow me say to you just what did work. Your writing is definitely quite powerful and this is most likely the reason why I am making an effort in order to opine. I do not make it a regular habit of doing that. Next, despite the fact that I can notice the jumps in reasoning you come up with, I am not necessarily confident of how you appear to connect the ideas that produce the actual final result. For the moment I will yield to your issue but trust in the near future you actually connect your dots much better.
نكهات الشيشة الالكترونية , فيب نكهات فيب شيشة الكترونية هو عبارة عن سائل يتم استخدامه في أجهزة الشيشة الإلكترونية. يتكون السائل من مجموعة متنوعة من المكونات بما في ذلك
مزاج , شيشةمزاج هو علامة تجارية تتخصص في صناعة وتوريد الشيشة ومستلزماتها. تتميز علامة التجارية بتصميماتها المبتكرة والعصرية، وجودة منتجاتها العالية، وتجربة العملاء
I dugg some of you post as I cogitated they were extremely helpful handy
Dịch vụ thám tử chuyên cung cấp giải pháp điều tra, cung cấp thông tin sự thật an toàn, bảo mật và tuân thủ pháp luật, giúp khách hàng thu thập thông tin chứng cứ và tư vấn giải quyết vấn đề đúng pháp luật mà không vi phạm đến quyền lợi của bất kỳ cá nhân nào.
Its like you read my mind! You appear to know so much about this, like you wrote the book in it or something. I think that you could do with some pics to drive the message home a bit, but instead of that, this is excellent blog. A fantastic read. I’ll certainly be back.
Thankyou for helping out, superb info .
I view something really special in this site.
I got what you intend, thankyou for posting.Woh I am thankful to find this website through google.
Good V I should certainly pronounce, impressed with your web site. I had no trouble navigating through all tabs as well as related information ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or anything, web site theme . a tones way for your customer to communicate. Excellent task..
I loved as much as you will receive carried out right here. The sketch is tasteful, your authored subject matter stylish. nonetheless, you command get got an nervousness over that you wish be delivering the following. unwell unquestionably come more formerly again since exactly the same nearly a lot often inside case you shield this hike.
I went over this web site and I believe you have a lot of wonderful information, saved to my bookmarks (:.
Glad to be one of the visitors on this awing site : D.
Very clean website , appreciate it for this post.
Absolutely written subject material, thanks for information .
You have brought up a very superb points, thanks for the post.
Hiya very nice web site!! Man .. Excellent .. Superb .. I will bookmark your blog and take the feeds also…I am happy to seek out numerous useful information here in the post, we want work out more techniques on this regard, thank you for sharing. . . . . .
مزاج , شيشةمزاج هو علامة تجارية تتخصص في صناعة وتوريد الشيشة ومستلزماتها. تتميز علامة التجارية بتصميماتها المبتكرة والعصرية، وجودة منتجاتها العالية، وتجربة العملاء
نكهات الشيشة الالكترونية , فيب نكهات فيب شيشة الكترونية هو عبارة عن سائل يتم استخدامه في أجهزة الشيشة الإلكترونية. يتكون السائل من مجموعة متنوعة من المكونات بما في ذلك
مزاج , شيشةمزاج هو علامة تجارية تتخصص في صناعة وتوريد الشيشة ومستلزماتها. تتميز علامة التجارية بتصميماتها المبتكرة والعصرية، وجودة منتجاتها العالية، وتجربة العملاء
Velbett – Link login – Daftar – Alternatif Slot Gacor Server thailand terpercaya di Indonesia. Velbett Memiliki Permainan slot gacor, Live casino, Bola Parlay mix, Dan Togel.
Velbett – Link login – Daftar – Alternatif Slot Gacor Server thailand terpercaya di Indonesia. Velbett Memiliki Permainan slot gacor, Live casino, Bola Parlay mix, Dan Togel.
I was very pleased to find this web-site.I wanted to thanks for your time for this wonderful read!! I definitely enjoying every little bit of it and I have you bookmarked to check out new stuff you blog post.
Oh my goodness! a tremendous article dude. Thanks Nevertheless I’m experiencing concern with ur rss . Don’t know why Unable to subscribe to it. Is there anybody getting similar rss downside? Anybody who is aware of kindly respond. Thnkx
Great items from you, man. I’ve understand your stuff previous to and you’re simply extremely magnificent. I actually like what you have obtained here, really like what you’re stating and the best way through which you say it. You’re making it enjoyable and you continue to care for to keep it wise. I cant wait to learn much more from you. This is really a terrific web site.
Youre so cool! I dont suppose Ive read something like this before. So nice to search out any person with some unique ideas on this subject. realy thank you for starting this up. this website is one thing that is wanted on the web, someone with slightly originality. helpful job for bringing something new to the web!
you’ve got an amazing weblog here! would you prefer to make some invite posts on my blog?
Go88 tự hào thu hút hàng triệu người chơi tham gia mỗi ngày bởi những ưu điểm nổi bật, khẳng định vị thế sân chơi cá cược uy tín và đẳng cấp trên thị trường https://go88app.link/
F*ckin’ remarkable issues here. I am very satisfied to peer your article. Thanks so much and i’m having a look forward to touch you. Will you kindly drop me a e-mail?
whoah this blog is fantastic i love reading your posts. Keep up the good work! You know, many people are looking around for this info, you can help them greatly.
Its excellent as your other content : D, appreciate it for posting.
Fantastic beat ! I wish to apprentice while you amend your web site, how could i subscribe for a blog website? The account aided me a acceptable deal. I had been tiny bit acquainted of this your broadcast provided bright clear idea
What’s Going down i’m new to this, I stumbled upon this I’ve discovered It absolutely useful and it has helped me out loads. I hope to give a contribution & assist different customers like its helped me. Good job.
Boost your website’s SEO with premium quality backlinks, including niche-specific casino backlinks. Enhance your site’s authority and improve your search engine rankings with our high-quality, powerful backlinks. Perfect for websites looking to gain a competitive edge!
Some truly wonderful information, Sword lily I observed this. “Be true to your work, your word, and your friend.” by Henry David Thoreau.
I would like to show my appreciation to this writer just for rescuing me from this particular condition. Because of surfing throughout the world wide web and finding recommendations which were not productive, I figured my life was well over. Existing without the presence of approaches to the difficulties you’ve fixed through the review is a crucial case, and the ones that could have adversely damaged my career if I had not noticed your web site. Your knowledge and kindness in handling the whole lot was crucial. I am not sure what I would have done if I had not come across such a thing like this. I can also at this time look ahead to my future. Thanks for your time so much for the skilled and result oriented guide. I won’t be reluctant to recommend your blog post to any person who wants and needs assistance on this problem.
There are some interesting time limits on this article but I don’t know if I see all of them heart to heart. There is some validity however I’ll take maintain opinion until I look into it further. Good article , thanks and we want more! Added to FeedBurner as properly
You got a very excellent website, Glad I noticed it through yahoo.
Attractive section of content. I just stumbled upon your web site and in accession capital to assert that I acquire actually enjoyed account your blog posts. Any way I will be subscribing to your augment and even I achievement you access consistently fast.
I’m not sure exactly why but this website is loading very slow for me. Is anyone else having this problem or is it a problem on my end? I’ll check back later and see if the problem still exists.
Thank you for sharing excellent informations. Your web site is very cool. I am impressed by the details that you have on this web site. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for extra articles. You, my friend, ROCK! I found just the information I already searched everywhere and just could not come across. What an ideal web-site.
Great blog here! Also your web site loads up very fast! What host are you using? Can I get your affiliate link to your host? I wish my site loaded up as quickly as yours lol
BANDARBOLA855 sebuah situs judi online yang telah eksis sejak lebih dari 8 tahun, berfokus pada penyediaan layanan taruhan slot online, bola online dan permainan judi lainnya. Sebagai bandar bola online terbaik, BANDARBOLA855 menawarkan pengalaman bermain yang aman dan menguntungkan bagi para pemain di seluruh Indonesia.
I like this website its a master peace ! Glad I detected this on google .
I like this web site very much so much wonderful info .
BANDARBOLA855 : Situs Judi Bola Online Resmi Terbesar di Indonesia
It’s actually a great and useful piece of information. I’m glad that you simply shared this useful information with us. Please stay us informed like this. Thank you for sharing.
What i don’t realize is actually how you’re not really much more well-liked than you might be right now. You’re so intelligent. You realize thus significantly relating to this subject, produced me personally consider it from so many varied angles. Its like men and women aren’t fascinated unless it is one thing to accomplish with Lady gaga! Your own stuffs nice. Always maintain it up!
Those are yours alright! . We at least need to get these people stealing images to start blogging! They probably just did a image search and grabbed them. They look good though!
Rattling fantastic info can be found on web blog. “Society produces rogues, and education makes one rogue more clever than another.” by Oscar Fingall O’Flahertie Wills Wilde.
kantorbola88 merupakan penyedia jasa games online yang sangat populer di indonesia saat ini, kantor bola juga memiliki ratting yang sangat tinggi
Really Appreciate this post, how can I make is so that I receive an email whenever you publish a fresh post?
Hello, i think that i saw you visited my website so i came to “go back the prefer”.I’m trying to find issues to improve my web site!I assume its adequate to use a few of your ideas!!
Greetings from Ohio! I’m bored at work so I decided to check out your blog on my iphone during lunch break. I really like the knowledge you provide here and can’t wait to take a look when I get home. I’m amazed at how fast your blog loaded on my cell phone .. I’m not even using WIFI, just 3G .. Anyhow, very good blog!
Pretty component of content. I simply stumbled upon your weblog and in accession capital to claim that I acquire in fact enjoyed account your blog posts. Anyway I will be subscribing on your feeds and even I achievement you get entry to consistently quickly.
Some really interesting information, well written and broadly speaking user pleasant.
Hello there, just became alert to your blog through Google, and found that it’s really informative. I am gonna watch out for brussels. I will appreciate if you continue this in future. Numerous people will be benefited from your writing. Cheers!
of course like your web site but you need to check the spelling on several of your posts. Several of them are rife with spelling issues and I find it very troublesome to tell the truth nevertheless I will certainly come back again.
송티비에서 고화질 실시간 스포츠중계를 즐기세요. 해외축구중계, 야구무료중계, NBA농구중계, 스포츠무료중계 등 국내외 다양한 스포츠 경기를 무료로 시청할 수 있습니다. 24시간 안정적인 서비스로 스포츠 중계의 진수를 경험하세요!
Hello, i think that i noticed you visited my web site thus i got here to “go back the want”.I am trying to find issues to improve my site!I suppose its good enough to use some of your ideas!!
Magnificent items from you, man. I’ve keep in mind your stuff prior to and you are simply too wonderful. I really like what you have got right here, certainly like what you’re saying and the best way in which you are saying it. You are making it enjoyable and you still care for to stay it sensible. I can not wait to learn far more from you. This is actually a wonderful website.
Some truly interesting info , well written and broadly speaking user pleasant.
I like this web site so much, saved to favorites.
As I website possessor I believe the subject material here is very excellent, thankyou for your efforts.
Yay google is my king aided me to find this great web site! .
I love reading and I believe this website got some truly utilitarian stuff on it! .
I was curious if you ever considered changing the layout of your site? Its very well written; I love what youve got to say. But maybe you could a little more in the way of content so people could connect with it better. Youve got an awful lot of text for only having one or 2 pictures. Maybe you could space it out better?
I am glad to be a visitor of this consummate site! , thanks for this rare information! .
I’d perpetually want to be update on new articles on this website , saved to favorites! .
You really make it seem really easy with your presentation but I find this matter to be really something which I feel I would by no means understand. It kind of feels too complex and extremely large for me. I am taking a look ahead for your subsequent submit, I’ll attempt to get the hang of it!
magnificent post, very informative. I wonder why the other experts of this sector do not notice this. You must continue your writing. I am sure, you have a great readers’ base already!
I’d should verify with you here. Which isn’t something I usually do! I take pleasure in reading a publish that can make people think. Also, thanks for permitting me to comment!
You should participate in a contest for one of the best blogs on the web. I’ll recommend this site!
Hi there! This is kind of off topic but I need some help from an established blog. Is it very difficult to set up your own blog? I’m not very techincal but I can figure things out pretty quick. I’m thinking about creating my own but I’m not sure where to begin. Do you have any tips or suggestions? Many thanks
Excellent beat ! I would like to apprentice while you amend your web site, how can i subscribe for a blog site? The account helped me a acceptable deal. I had been a little bit acquainted of this your broadcast provided bright clear idea
you are really a good webmaster. The web site loading speed is amazing. It seems that you are doing any unique trick. In addition, The contents are masterpiece. you have done a excellent job on this topic!
I regard something genuinely special in this internet site.
Hi , I do believe this is an excellent blog. I stumbled upon it on Yahoo , i will come back once again. Money and freedom is the best way to change, may you be rich and help other people.
I would like to thnkx for the efforts you’ve put in writing this site. I am hoping the same high-grade blog post from you in the upcoming as well. Actually your creative writing skills has encouraged me to get my own web site now. Really the blogging is spreading its wings rapidly. Your write up is a good example of it.
The next time I read a blog, I hope that it doesnt disappoint me as much as this one. I mean, I know it was my choice to read, but I actually thought youd have something interesting to say. All I hear is a bunch of whining about something that you could fix if you werent too busy looking for attention.
I¦ve learn some good stuff here. Definitely price bookmarking for revisiting. I wonder how so much effort you place to create any such fantastic informative site.
Wow! Thank you! I constantly needed to write on my site something like that. Can I take a part of your post to my site?
Wow! This can be one particular of the most useful blogs We have ever arrive across on this subject. Actually Excellent. I’m also an expert in this topic so I can understand your effort.
I will immediately clutch your rss as I can’t find your email subscription hyperlink or newsletter service. Do you have any? Kindly permit me know in order that I could subscribe. Thanks.
I don’t ordinarily comment but I gotta admit regards for the post on this great one : D.
I believe this web site holds some very excellent information for everyone : D.
Just wish to say your article is as surprising. The clarity in your post is just cool and i can assume you are an expert on this subject. Fine with your permission allow me to grab your RSS feed to keep updated with forthcoming post. Thanks a million and please continue the gratifying work.
A person essentially help to make seriously articles I would state. This is the very first time I frequented your web page and thus far? I amazed with the research you made to make this particular publish amazing. Magnificent job!
Thank you so much for providing individuals with such a splendid possiblity to read articles and blog posts from this website. It is usually so useful and also full of amusement for me personally and my office peers to search your blog at the very least three times weekly to see the new guidance you will have. Not to mention, I’m just actually motivated with all the amazing thoughts served by you. Selected two ideas on this page are essentially the most suitable we have had.
Klik Link Ini Di Jamin Dan Rasakan Cuan JP Banget!!
Very interesting info!Perfect just what I was looking for!
I¦ve recently started a website, the info you offer on this web site has helped me tremendously. Thanks for all of your time & work.
Hello! I could have sworn I’ve been to this blog before but after browsing through some of the post I realized it’s new to me. Anyways, I’m definitely happy I found it and I’ll be book-marking and checking back frequently!
I’m not that much of a online reader to be honest but your blogs really nice, keep it up! I’ll go ahead and bookmark your site to come back down the road. All the best
Super-Duper website! I am loving it!! Will be back later to read some more. I am bookmarking your feeds also
That is really fascinating, You’re an excessively professional blogger. I’ve joined your rss feed and look forward to looking for extra of your magnificent post. Also, I have shared your web site in my social networks!
Valuable information. Lucky me I found your website by accident, and I’m shocked why this accident didn’t happened earlier! I bookmarked it.
I don’t even understand how I stopped up right here, but I believed this submit was great. I don’t realize who you might be however definitely you are going to a famous blogger in case you aren’t already 😉 Cheers!
Aw, this was a very nice post. In thought I wish to put in writing like this moreover – taking time and precise effort to make an excellent article… however what can I say… I procrastinate alot and in no way appear to get something done.
Real clean internet site, thankyou for this post.
you have got an incredible weblog right here! would you wish to make some invite posts on my weblog?
Hi my family member! I want to say that this post is awesome,great written and include approximately all important infosI’d like to see more posts like this Feel free to surf to my blog post :: バカラ
Thank you, I have recently been searching for info about this topic for ages and yours is the greatest I have discovered so far. But, what about the conclusion? Are you sure about the source?
I believe other website owners should take this internet site as an model, very clean and excellent user friendly pattern.
I am not really fantastic with English but I come up this real easy to read .
I have been surfing online greater than three hours nowadays, but I by no means discovered any interesting article like yours. It is beautiful price sufficient for me. In my view, if all website owners and bloggers made just right content as you did, the net might be much more helpful than ever before. “Wherever they burn books, they will also, in the end, burn people.” by Heinrich Heine.
There are definitely a number of details like that to take into consideration. That may be a great point to convey up. I supply the thoughts above as normal inspiration however clearly there are questions like the one you carry up where an important thing can be working in trustworthy good faith. I don?t know if best practices have emerged round issues like that, but I am certain that your job is clearly identified as a fair game. Both girls and boys really feel the impression of only a second’s pleasure, for the remainder of their lives.
Very interesting info !Perfect just what I was searching for!
istanbul escort
Hi just wanted to give you a brief heads up and let you know a few of the images aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different internet browsers and both show the same results.
istanbul escort
istanbul escort
very good put up, i definitely love this web site, keep on it
My coder is trying to persuade me to move to .net from PHP. I have always disliked the idea because of the costs. But he’s tryiong none the less. I’ve been using WordPress on various websites for about a year and am concerned about switching to another platform. I have heard great things about blogengine.net. Is there a way I can import all my wordpress posts into it? Any help would be really appreciated!
It’s a shame you don’t have a donate button! I’d certainly donate to this excellent blog! I guess for now i’ll settle for book-marking and adding your RSS feed to my Google account. I look forward to new updates and will talk about this blog with my Facebook group. Talk soon!
I love it when people come together and share opinions, great blog, keep it up.
Awsome article and right to the point. I don’t know if this is actually the best place to ask but do you folks have any ideea where to employ some professional writers? Thanks 🙂
Woh I like your content, bookmarked! .
快连,快连下载,快连vpn,快连vpn下载,快连官方,快连官方下载,letsvpn,letsvpn download
Hey, I think your website might be having browser compatibility issues. When I look at your blog in Opera, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, superb blog!
Hi, I think your blog might be having browser compatibility issues. When I look at your blog in Opera, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, excellent blog!
快连,快连下载,快连vpn,快连vpn下载,快连官方,快连官方下载,letsvpn,letsvpn download
Wohh precisely what I was looking for, appreciate it for putting up.
It is the best time to make some plans for the longer term and it’s time to be happy. I’ve read this put up and if I could I wish to recommend you few fascinating things or tips. Maybe you can write next articles regarding this article. I desire to read more things about it!
快连,快连下载,快连vpn,快连vpn下载,快连官方,快连官方下载,letsvpn,letsvpn download
Hi there very cool web site!! Guy .. Excellent .. Wonderful .. I’ll bookmark your blog and take the feeds alsoKI am glad to find numerous useful information right here within the publish, we want work out more strategies in this regard, thanks for sharing. . . . . .
快连,快连下载,快连vpn,快连vpn下载,快连官方,快连官方下载,letsvpn,letsvpn download
Hello would you mind sharing which blog platform you’re using? I’m going to start my own blog soon but I’m having a tough time deciding between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your design and style seems different then most blogs and I’m looking for something unique. P.S Apologies for being off-topic but I had to ask!
Greetings I am so glad I found your web site, I really found you by error, while I was browsing on Aol for something else, Regardless I am here now and would just like to say thanks for a marvelous post and a all round exciting blog (I also love the theme/design), I don’t have time to read through it all at the moment but I have saved it and also added in your RSS feeds, so when I have time I will be back to read a lot more, Please do keep up the excellent work.
Hello. magnificent job. I did not expect this. This is a splendid story. Thanks!
Great – I should certainly pronounce, impressed with your website. I had no trouble navigating through all the tabs as well as related information ended up being truly simple to do to access. I recently found what I hoped for before you know it at all. Quite unusual. Is likely to appreciate it for those who add forums or anything, website theme . a tones way for your client to communicate. Nice task.
Very interesting topic, regards for putting up.
Gerçek Bursa escort bayan görükle eskort kız arayanlar , güncel sayfamız ile yeni escort bayanlar ile tanışın. Sınırsız Bursa Görükle Escort Sitemizde
F*ckin’ amazing things here. I am very glad to see your article. Thanks a lot and i am looking forward to contact you. Will you please drop me a mail?
Gerçek Bursa escort bayan görükle eskort kız arayanlar , güncel sayfamız ile yeni escort bayanlar ile tanışın. Sınırsız Bursa Görükle Escort Sitemizde
I¦ve learn several excellent stuff here. Definitely price bookmarking for revisiting. I surprise how a lot attempt you set to create any such fantastic informative site.
I just couldn’t depart your site before suggesting that I really enjoyed the standard info a person provide for your visitors? Is gonna be back often to check up on new posts
Hi, Neat post. There’s an issue along with your website in web explorer, might check thisK IE still is the marketplace chief and a huge section of other folks will leave out your fantastic writing because of this problem.
Well I truly liked studying it. This information offered by you is very useful for good planning.
I like the helpful information you provide in your articles. I will bookmark your weblog and check again here regularly. I’m quite certain I will learn lots of new stuff right here! Good luck for the next!
Le pizzerie a torino zona per zona dove trovarle”
You have brought up a very good details , thankyou for the post.
Real fantastic information can be found on website.
Very interesting information!Perfect just what I was looking for!
I appreciate your piece of work, thankyou for all the informative content.
I gotta bookmark this web site it seems handy extremely helpful
Pretty section of content. I just stumbled upon your website and in accession capital to assert that I get in fact enjoyed account your blog posts. Any way I will be subscribing to your feeds and even I achievement you access consistently rapidly.
As a Newbie, I am always exploring online for articles that can be of assistance to me. Thank you
You could definitely see your skills within the paintings you write. The sector hopes for even more passionate writers like you who are not afraid to mention how they believe. All the time go after your heart.
The subsequent time I learn a weblog, I hope that it doesnt disappoint me as much as this one. I mean, I do know it was my choice to read, however I truly thought youd have something interesting to say. All I hear is a bunch of whining about one thing that you would repair when you werent too busy in search of attention.
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
I like what you guys are up too. Such intelligent work and reporting! Carry on the superb works guys I have incorporated you guys to my blogroll. I think it will improve the value of my web site 🙂
Hey there! This is kind of off topic but I need some advice from an established blog. Is it very hard to set up your own blog? I’m not very techincal but I can figure things out pretty quick. I’m thinking about setting up my own but I’m not sure where to begin. Do you have any points or suggestions? Cheers
I haven?¦t checked in here for some time because I thought it was getting boring, but the last few posts are great quality so I guess I will add you back to my everyday bloglist. You deserve it my friend 🙂
I would like to thank you for the efforts you’ve put in writing this site. I’m hoping the same high-grade site post from you in the upcoming also. In fact your creative writing skills has encouraged me to get my own blog now. Really the blogging is spreading its wings quickly. Your write up is a good example of it.
I would like to thnkx for the efforts you have put in writing this blog. I am hoping the same high-grade blog post from you in the upcoming as well. In fact your creative writing abilities has inspired me to get my own blog now. Really the blogging is spreading its wings quickly. Your write up is a good example of it.
Hello.This post was extremely remarkable, particularly since I was browsing for thoughts on this subject last Saturday.
Hello there, just became aware of your blog through Google, and found that it’s really informative. I am going to watch out for brussels. I’ll appreciate if you continue this in future. Numerous people will be benefited from your writing. Cheers!
Jnetoto Situs Daftar Bandar Toto Macau Hadiah Terbesar 2024
Oh my goodness! Aweesome article dude! Thank you,
However I aam encountering difficulties with your RSS.
I don’t understand the reason why I can’t subscribe to it.
Is there anybody having the same RSS issues? Anyone who knows the solution can you kindly respond?
Thanks!!
Here is my web blog :: istanbul escort
you are really a good webmaster. The website loading speed is amazing. It seems that you’re doing any unique trick. Furthermore, The contents are masterwork. you’ve done a wonderful job on this topic!
bursa escort,görükle escort
My brother recommended I might like this website. He was entirely right. This post actually made my day. You cann’t imagine simply how much time I had spent for this information! Thanks!
Hi my friend! I wish to say that this article is amazing, nice written and include almost all vital infos. I would like to see more posts like this.
Thank you for another informative web site. Where else could I get that type of info written in such an ideal way? I’ve a project that I am just now working on, and I’ve been on the look out for such info.
I am glad to be one of several visitors on this outstanding website (:, appreciate it for posting.
I got what you intend, thankyou for posting.Woh I am pleased to find this website through google. “Delay is preferable to error.” by Thomas Jefferson.
I liked as much as you’ll obtain performed right here. The cartoon is tasteful, your authored material stylish. nevertheless, you command get bought an edginess over that you would like be handing over the following. sick unquestionably come further beforehand again as exactly the similar just about very regularly inside of case you shield this hike.
Hello ulisboa.pt admin, Your posts are always well thought out.
I believe this internet site contains very great indited subject matter articles.
Yes! Finaally something about escort.
Here is my web-site: istanbul eskort
https://sarhim.ru/wp-includes/pgs/1xbet_promokod_54.html
Thank you for sharing with us, I believe this website truly stands out : D.
Very efficiently written post. It will be helpful to everyone who utilizes it, including myself. Keep doing what you are doing – can’r wait to read more posts.
Some truly rattling work on behalf of the owner of this site, utterly outstanding written content.
An interesting discussion is worth comment. I think that you should write more on this topic, it might not be a taboo subject but generally people are not enough to speak on such topics. To the next. Cheers
Very great post. I just stumbled upon your blog and wanted to mention that I’ve really enjoyed surfing around your blog posts. After all I’ll be subscribing for your rss feed and I am hoping you write once more soon!
Hello my loved one! I want to say that this post is amazing, nice written and include approximately all vital infos. I¦d like to peer extra posts like this .
Rattling great information can be found on web site.
What i do not understood is actually how you’re not actually much more well-liked than you may be right now. You are so intelligent. You realize therefore considerably relating to this subject, made me personally consider it from a lot of varied angles. Its like men and women aren’t fascinated unless it is one thing to accomplish with Lady gaga! Your own stuffs excellent. Always maintain it up!
Sex Fuck
Discover Prime Bot, the ultimate crypto sniper bot offering advanced AI features like sniping, front-running, MEV and more. Supports Ethereum, Solana, BSC, and over 60 chains.
Have you ever thought about including a little bit more than just your articles? I mean, what you say is important and all. But imagine if you added some great graphics or video clips to give your posts more, “pop”! Your content is excellent but with pics and videos, this blog could undeniably be one of the greatest in its field. Wonderful blog!
I used to be recommended this website by means of my cousin. I am now not sure whether this post is written through him as no one else recognise such certain approximately my difficulty. You are amazing! Thanks!
Everyone loves what you guys are usually up too. This sort of clever work and reporting! Keep up the wonderful works guys I’ve you guys to my blogroll.
Greetings! Very helpful advice on this article! It is the little changes that make the biggest changes. Thanks a lot for sharing!
Oh my goodness! an incredible article dude. Thanks Nevertheless I’m experiencing problem with ur rss . Don’t know why Unable to subscribe to it. Is there anybody getting equivalent rss drawback? Anyone who is aware of kindly respond. Thnkx
Some truly wondrous work on behalf of the owner of this web site, utterly great subject material.
I regard something genuinely special in this web site.
You are my aspiration, I have few blogs and often run out from to brand.
I’ve been exploring for a little bit for any high-quality articles or blog posts on this kind of area . Exploring in Yahoo I at last stumbled upon this web site. Reading this info So i’m happy to convey that I have an incredibly good uncanny feeling I discovered exactly what I needed. I most certainly will make certain to do not forget this site and give it a glance regularly.
whoah this blog is magnificent i love reading your posts. Keep up the great work! You know, lots of people are looking around for this info, you can help them greatly.
Real nice pattern and excellent content material, absolutely nothing else we require : D.
Wow! Thank you! I permanently wanted to write on my blog something like that. Can I include a fragment of your post to my website?
Thank you for sharing with us, I believe this website genuinely stands out : D.
Telefono Erotico Per Donne, Godere non è mai un Peccato, è un Piacere. Un servizo, discreto, Riservato Esclusivo per te, per i momenti di piacere al Telefono Erotico Per Donne. L'Unica Linea Erotica per Donne in Italia, che regala minuti di piacere al telefono erotico.
I’ve been exploring for a little for any high quality articles or blog posts on this sort of area . Exploring in Yahoo I at last stumbled upon this site. Reading this info So i’m happy to convey that I have an incredibly good uncanny feeling I discovered just what I needed. I most certainly will make certain to do not forget this web site and give it a look on a constant basis.
I am very happy to read this. This is the kind of manual that needs to be given and not the random misinformation that is at the other blogs. Appreciate your sharing this greatest doc.
Hello. remarkable job. I did not expect this. This is a great story. Thanks!
Its great as your other content : D, regards for posting.
Just what I was searching for, appreciate it for putting up.
certainly like your website however you have to test the spelling on quite a few of your posts. Several of them are rife with spelling problems and I find it very troublesome to tell the reality then again I?¦ll surely come back again.
Simply a smiling visitor here to share the love (:, btw great design. “The price one pays for pursuing a profession, or calling, is an intimate knowledge of its ugly side.” by James Arthur Baldwin.
Absolutely pent content material, thank you for information. “Life is God’s novel. Let him write it.” by Isaac Bashevis Singer.
I am often to running a blog and i really recognize your content. The article has actually peaks my interest. I’m going to bookmark your site and hold checking for brand new information.
Hi! Do you use Twitter? I’d like to follow you if that would be ok. I’m undoubtedly enjoying your blog and look forward to new posts.
You made certain fine points there. I did a search on the subject and found most persons will consent with your blog.
Very interesting topic, regards for posting. “Nothing great was ever achieved without enthusiasm.” by George Ellis.
This really answered my drawback, thank you!
Its like you learn my mind! You seem to grasp a lot approximately this, like you wrote the e book in it or something. I think that you could do with some percent to force the message home a bit, however other than that, that is excellent blog. An excellent read. I’ll certainly be back.
hello!,I like your writing very much! share we communicate more about your article on AOL? I require an expert on this area to solve my problem. May be that’s you! Looking forward to see you.
Well I sincerely enjoyed reading it. This article offered by you is very effective for good planning.
Great wordpress blog here.. It’s hard to find quality writing like yours these days. I really appreciate people like you! take care
I’d have to examine with you here. Which is not one thing I usually do! I take pleasure in reading a post that may make folks think. Additionally, thanks for permitting me to comment!
Some genuinely excellent posts on this website, thanks for contribution. “My salad days, When I was green in judgment.” by William Shakespeare.
Your place is valueble for me. Thanks!…
I’ve been surfing on-line more than three hours these days, but I by no means found any interesting article like yours. It is lovely worth enough for me. Personally, if all web owners and bloggers made excellent content as you did, the web can be much more helpful than ever before. “A winner never whines.” by Paul Brown.
I’ve been absent for a while, but now I remember why I used to love this blog. Thank you, I will try and check back more frequently. How frequently you update your website?
Generally I don’t read post on blogs, but I would like to say that this write-up very forced me to check out and do so! Your writing style has been surprised me. Thank you, quite nice post.
What¦s Happening i’m new to this, I stumbled upon this I’ve found It absolutely helpful and it has aided me out loads. I hope to contribute & help other users like its helped me. Great job.
I’m a Professional SEO Expert with over 10 years of industry experience, an SEO Specialist in White Hat SEO techniques, SMM, SEM, and Web Traffic, and a High Authority Backlinks/building expert. Please feel free to get in touch today and we can discuss your project and what you want to achieve
Pretty nice post. I just stumbled upon your weblog and wished to say that I’ve truly enjoyed surfing around your blog posts. After all I’ll be subscribing to your feed and I hope you write again soon!
I have been surfing online greater than 3 hours nowadays, yet I never found any attention-grabbing article like yours. It’s beautiful value enough for me. Personally, if all site owners and bloggers made good content material as you did, the net will likely be a lot more helpful than ever before.
The #1 funeral wholesale from Europe | Dropshipping | Shop for cremation urns, coffins, funeral flowers, hearses and a lot more | Check our website”
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
F*ckin’ tremendous things here. I am very glad to see your post. Thanks a lot and i’m looking forward to contact you. Will you please drop me a e-mail?
It is best to participate in a contest for probably the greatest blogs on the web. I’ll recommend this web site!
I like this post, enjoyed this one appreciate it for posting. “Fear not for the future, weep not for the past.” by Percy Bysshe Shelley.
I couldn’t resist commenting
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
Thank you for every other great article. The place else could anybody get that kind of information in such a perfect approach of writing? I’ve a presentation subsequent week, and I’m at the look for such info.
Great website. Plenty of useful information here. I am sending it to some pals ans also sharing in delicious. And certainly, thank you on your effort!
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
Prime Bot is designed for sniping, front-running, and MEV across multiple blockchains. It offers unmatched efficiency, accuracy, and security with advanced AI, providing essential tools for both novice and experienced traders.
Do you mind if I quote a few of your posts as long as I provide credit and sources back to your site? My blog is in the very same area of interest as yours and my visitors would really benefit from some of the information you present here. Please let me know if this alright with you. Cheers!
Prime Bot is designed for sniping, front-running, and MEV across multiple blockchains. It offers unmatched efficiency, accuracy, and security with advanced AI, providing essential tools for both novice and experienced traders.
After study a few of the blog posts on your website now, and I truly like your way of blogging. I bookmarked it to my bookmark website list and will be checking back soon. Pls check out my web site as well and let me know what you think.
I’m usually to running a blog and i really appreciate your content. The article has really peaks my interest. I’m going to bookmark your web site and keep checking for new information.
There is noticeably a bundle to know about this. I assume you made certain nice points in features also.
PACKMAN is a brand that offers a line of disposable vape pens and cartridges made with high-quality cannabis oil and concentrates. The key features of PACKMAN
Perfectly pent articles, Really enjoyed looking at.
PACKMAN is a brand that offers a line of disposable vape pens and cartridges made with high-quality cannabis oil and concentrates. The key features of PACKMAN
PACKMAN is a brand that offers a line of disposable vape pens and cartridges made with high-quality cannabis oil and concentrates. The key features of PACKMAN
Just wanna admit that this is very beneficial, Thanks for taking your time to write this.
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
Virtually all of whatever you articulate happens to be supprisingly legitimate and it makes me ponder why I hadn’t looked at this with this light previously. This article truly did turn the light on for me personally as far as this subject matter goes. Nonetheless there is 1 point I am not too cozy with and while I make an effort to reconcile that with the main theme of the position, allow me see exactly what the rest of your visitors have to point out.Very well done.
Buy Herbal Incense Online at USA Herbal Incense. We are the number one Herbal Incense Store in USA. Selling Top Quality Herbal Incense online to K2 Lovers
An interesting dialogue is price comment. I think that it is best to write extra on this subject, it might not be a taboo subject but generally people are not enough to speak on such topics. To the next. Cheers
situs slot gacor kolam4d.
I’m not sure where you are getting your info, but great topic. I needs to spend some time learning more or understanding more. Thanks for great info I was looking for this info for my mission.
WONDERFUL Post.thanks for share..extra wait .. …
Great blog! Do you have any helpful hints for aspiring writers? I’m hoping to start my own blog soon but I’m a little lost on everything. Would you recommend starting with a free platform like WordPress or go for a paid option? There are so many options out there that I’m totally confused .. Any ideas? Thanks!
Hey! I just wanted to ask if you ever have any issues with hackers? My last blog (wordpress) was hacked and I ended up losing many months of hard work due to no data backup. Do you have any solutions to prevent hackers?
telefono erotico per donne,telefono erotico per donne,linea erotica per donne,linea erotica per donne
It’s actually a great and useful piece of info. I’m glad that you simply shared this useful info with us. Please keep us informed like this. Thanks for sharing.
Hey there! This is my 1st comment here so I just wanted to give a quick shout out and say I really enjoy reading through your posts. Can you recommend any other blogs/websites/forums that go over the same subjects? Thank you so much!
Your house is valueble for me. Thanks!…
telefono erotico per donne,telefono erotico per donne,linea erotica per donne,linea erotica per donne
It?¦s really a great and helpful piece of info. I am happy that you just shared this useful information with us. Please stay us up to date like this. Thank you for sharing.
excellent points altogether, you simply gained a brand new reader. What would you recommend in regards to your post that you made a few days ago? Any positive?
I truly enjoy looking through on this website , it has got wonderful posts.
I’ll immediately snatch your rss as I can’t find your e-mail subscription link or e-newsletter service. Do you’ve any? Please let me recognise in order that I could subscribe. Thanks.
Those are yours alright! . We at least need to get these people stealing images to start blogging! They probably just did a image search and grabbed them. They look good though!
Hello! Would you mind if I share your blog with my facebook group? There’s a lot of folks that I think would really appreciate your content. Please let me know. Thank you
I am really impressed with your writing skills as well as with the layout on your blog. Is this a paid theme or did you customize it yourself? Anyway keep up the excellent quality writing, it is rare to see a nice blog like this one today..
I do agree with all the ideas you have presented in your post. They’re really convincing and will definitely work. Still, the posts are very short for novices. Could you please extend them a bit from next time? Thanks for the post.
Thank you, I’ve just been looking for info about this topic for ages and yours is the best I’ve discovered so far. But, what about the bottom line? Are you sure about the source?
istanbul escort anadolu yakası escort , avrupa yakası escort
Hello There. I found your blog using msn. This is a really well written article. I will make sure to bookmark it and come back to read more of your useful info. Thanks for the post. I will definitely comeback.
Nice post. I was checking constantly this blog and I’m impressed! Very useful info specifically the last part 🙂 I care for such info much. I was seeking this particular information for a very long time. Thank you and best of luck.
Hello.This article was extremely remarkable, especially since I was investigating for thoughts on this subject last couple of days.
I appreciate, cause I found just what I was looking for. You have ended my 4 day long hunt! God Bless you man. Have a great day. Bye
naturally like your web site but you need to test the spelling on several of your posts. Several of them are rife with spelling issues and I in finding it very bothersome to inform the reality however I’ll surely come back again.
Lovely just what I was looking for.Thanks to the author for taking his time on this one.
That is very interesting, You are a very professional blogger. I’ve joined your feed and stay up for looking for extra of your magnificent post. Also, I have shared your website in my social networks!
The other day, while I was at work, my sister stole my iphone and tested to see if it can survive a 40 foot drop, just so she can be a youtube sensation. My iPad is now broken and she has 83 views. I know this is completely off topic but I had to share it with someone!
I dugg some of you post as I cerebrated they were very beneficial very beneficial
I as well think thus, perfectly composed post! .
It is really a nice and helpful piece of information. I am glad that you shared this useful information with us. Please keep us up to date like this. Thanks for sharing.
Hi , I do believe this is an excellent blog. I stumbled upon it on Yahoo , i will come back once again. Money and freedom is the best way to change, may you be rich and help other people.
I?¦ve been exploring for a little bit for any high-quality articles or weblog posts on this kind of house . Exploring in Yahoo I at last stumbled upon this site. Studying this information So i?¦m happy to express that I have a very just right uncanny feeling I discovered just what I needed. I such a lot certainly will make certain to don?¦t overlook this web site and give it a look on a constant basis.
Of course, what a magnificent site and enlightening posts, I surely will bookmark your website.Best Regards!
Very interesting information!Perfect just what I was looking for!
Hi my loved one! I wish to say that this article is amazing, great written and include almost all vital infos. I’d like to see more posts like this.
Just want to say your article is as astounding. The clearness to your put up is simply great and i could suppose you are knowledgeable in this subject. Well with your permission let me to grasp your feed to stay up to date with drawing close post. Thank you a million and please keep up the rewarding work.
Wonderful blog! I found it while browsing on Yahoo News. Do you have any suggestions on how to get listed in Yahoo News? I’ve been trying for a while but I never seem to get there! Cheers
As a Newbie, I am constantly browsing online for articles that can aid me. Thank you
I simply wished to thank you very much all over again. I’m not certain the things I would have tried in the absence of those strategies contributed by you on that problem. This has been a real alarming dilemma in my opinion, but seeing a specialized approach you managed the issue took me to jump over happiness. I’m just grateful for the support and then trust you realize what a great job you are getting into educating men and women through your web blog. Most probably you haven’t met any of us.
you are really a good webmaster. The web site loading speed is incredible. It seems that you are doing any unique trick. Also, The contents are masterwork. you’ve done a wonderful job on this topic!
I’ll immediately grab your rss as I can’t find your email subscription link or e-newsletter service. Do you have any? Kindly let me know in order that I could subscribe. Thanks.
I truly enjoy reading on this website , it holds great posts.
It is really a nice and useful piece of information. I am satisfied that you just shared this helpful information with us. Please keep us informed like this. Thank you for sharing.
Way cool, some valid points! I appreciate you making this article available, the rest of the site is also high quality. Have a fun.
Hey! Quick question that’s totally off topic. Do you know how to make your site mobile friendly? My site looks weird when viewing from my iphone4. I’m trying to find a template or plugin that might be able to resolve this problem. If you have any suggestions, please share. Thank you!
Usually I do not read post on blogs, but I would like to say that this write-up very compelled me to try and do it! Your writing taste has been amazed me. Thanks, very nice article.
After examine a couple of of the blog posts on your website now, and I truly like your way of blogging. I bookmarked it to my bookmark website list and might be checking back soon. Pls try my website as properly and let me know what you think.
Youre so cool! I dont suppose Ive learn something like this before. So good to search out someone with some original ideas on this subject. realy thank you for starting this up. this website is something that is wanted on the web, someone with a bit originality. useful job for bringing something new to the web!
It is the best time to make a few plans for the long run and it’s time to be happy. I’ve read this submit and if I may I want to counsel you few attention-grabbing things or suggestions. Perhaps you can write subsequent articles referring to this article. I wish to read even more issues about it!
I¦ll immediately clutch your rss as I can’t find your e-mail subscription hyperlink or e-newsletter service. Do you’ve any? Kindly let me recognize so that I may just subscribe. Thanks.
Great ?V I should definitely pronounce, impressed with your site. I had no trouble navigating through all the tabs as well as related info ended up being truly easy to do to access. I recently found what I hoped for before you know it at all. Quite unusual. Is likely to appreciate it for those who add forums or anything, website theme . a tones way for your customer to communicate. Nice task..
Thank you for sharing excellent informations. Your website is so cool. I’m impressed by the details that you’ve on this blog. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for more articles. You, my friend, ROCK! I found simply the info I already searched all over the place and just couldn’t come across. What an ideal web site.
You are my inspiration , I own few blogs and very sporadically run out from to post : (.
Very well written post. It will be valuable to everyone who utilizes it, including myself. Keep doing what you are doing – can’r wait to read more posts.
You actually make it seem so easy with your presentation however I find
this matter to be really something that I think I’d by no means understand.
It seems too complicated and very extensive for me.
I am having a look ahead for your next submit, I’ll attempt to get the dangle of it!
What’s Taking place i am new to this, I stumbled upon this I have found It absolutely helpful and it has helped me out loads. I am hoping to contribute & assist different users like its aided me. Great job.
This paragraph will assist the internet users for building up new webpage or even a blog from start to end.
Here is my web page; pronerve 6 ingredients
I’m really inspired along with your writing abilities and also with the format to your blog. Is this a paid theme or did you customize it yourself? Either way keep up the nice quality writing, it’s uncommon to peer a great weblog like this one nowadays..
I do agree with all the ideas you have presented in your post. They are very convincing and will definitely work. Still, the posts are very short for newbies. Could you please extend them a little from next time? Thanks for the post.
Admiring the dedication you put into your site and in depth information you present. It’s nice to come across a blog every once in a while that isn’t the same old rehashed material. Great read! I’ve saved your site and I’m including your RSS feeds to my Google account.
You are my inspiration, I own few web logs and often run out from post :). “To die for a religion is easier than to live it absolutely.” by Jorge Luis Borges.
Hello my family member! I want to say that this post is awesome, great written and come with almost all vital infos. I would like to see extra posts like this .
Its good as your other blog posts : D, thanks for putting up. “In the spider-web of facts, many a truth is strangled.” by Paul Eldridge.
Please let me know if you’re looking for a article author for your site. You have some really great articles and I think I would be a good asset. If you ever want to take some of the load off, I’d absolutely love to write some material for your blog in exchange for a link back to mine. Please shoot me an email if interested. Regards!
Can I just say what a relief to find someone who actually knows what theyre talking about on the internet. You definitely know how to bring an issue to light and make it important. More people need to read this and understand this side of the story. I cant believe youre not more popular because you definitely have the gift.
It’s laborious to search out educated folks on this subject, however you sound like you already know what you’re speaking about! Thanks
Hi, i think that i saw you visited my website so i came to “return the favor”.I am attempting to find things to enhance my site!I suppose its ok to use a few of your ideas!!
Just wish to say your article is as astonishing. The clarity in your post is just great and i could assume you’re an expert on this subject. Well with your permission allow me to grab your feed to keep up to date with forthcoming post. Thanks a million and please keep up the gratifying work.
BUY FAVORITE DISPOSABLE To buy your favorite disposable vapes, you can explore various online platforms and vape shops that offer a wide selection of popular disposable vape products favorites disposable thc, favorite dispo , favorite 2g disposable BUY FAVORITES 2G DISPOSABLE favorites 2 gram disposable , by favorites disposable , favorites carts disposable ,favorites disposable
BUY FAVORITE DISPOSABLE To buy your favorite disposable vapes, you can explore various online platforms and vape shops that offer a wide selection of popular disposable vape products favorites disposable thc, favorite dispo , favorite 2g disposable BUY FAVORITES 2G DISPOSABLE favorites 2 gram disposable , by favorites disposable , favorites carts disposable ,favorites disposable
BUY FAVORITE DISPOSABLE To buy your favorite disposable vapes, you can explore various online platforms and vape shops that offer a wide selection of popular disposable vape products favorites disposable thc, favorite dispo , favorite 2g disposable BUY FAVORITES 2G DISPOSABLE favorites 2 gram disposable , by favorites disposable , favorites carts disposable ,favorites disposable
What i do not realize is if truth be told how you’re now not actually much more smartly-favored than you may be now. You’re so intelligent. You already know therefore significantly when it comes to this matter, produced me personally imagine it from a lot of varied angles. Its like men and women are not interested until it’s one thing to accomplish with Lady gaga! Your individual stuffs excellent. Always take care of it up!
hello!,I like your writing very much! share we communicate more about your post on AOL? I require a specialist on this area to solve my problem. May be that’s you! Looking forward to see you.
My spouse and i felt so thrilled that Louis could do his survey through your precious recommendations he discovered in your web pages. It is now and again perplexing to just possibly be offering guidelines that some other people could have been trying to sell. We keep in mind we have got the writer to appreciate for that. The explanations you made, the straightforward web site menu, the relationships your site aid to engender – it’s many impressive, and it’s letting our son in addition to the family consider that this situation is amusing, which is certainly very pressing. Thank you for all!
My brother suggested I may like this website. He was once totally right. This submit truly made my day. You cann’t consider just how a lot time I had spent for this information! Thank you!
Today, I went to the beachfront with my kids. I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She put the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear. She never wants to go back! LoL I know this is completely off topic but I had to tell someone!
Great line up. We will be linking to this great article on our site. Keep up the good writing.
Welcome to Fryd Extracts USA, where innovation meets satisfaction in every puff. Our Fryd Extracts Disposable Vape is a masterpiece of flavor and convenience.
1xbet promo code today pakistan
Welcome to Fryd Extracts USA, where innovation meets satisfaction in every puff. Our Disposable Vape is a masterpiece of flavor and convenience, designed for those who appreciate the finer things in life. Crafted with precision, each disposable vape delivers a seamless blend of rich, nuanced flavors that promise to elevate your vaping experience. Perfect for on-the-go moments or relaxing at home, our disposables offer a hassle- free journey into a world of exquisite taste and unmatched quality. Discover the essence of luxury vaping with Fryd Extracts Disposable Vape – your pocket-sized passport to a universe of flavor.
I got what you intend, thankyou for putting up.Woh I am glad to find this website through google. “Those who corrupt the public mind are just as evil as those who steal from the public.” by Theodor Wiesengrund Adorno.
Hi my friend! I wish to say that this post is awesome, great written and include almost all significant infos. I would like to look extra posts like this .
Hey! I could have sworn I’ve been to this blog before but after checking through some of the post I realized it’s new to me. Anyhow, I’m definitely happy I found it and I’ll be book-marking and checking back frequently!
To buy your favorite disposable vapes, you can explore various online platforms and vape shops that offer a wide selection of popular disposable vape products favorites disposable thc, favorite dispo , favorite 2g disposable
My spouse and i got very fortunate that Emmanuel managed to round up his homework via the ideas he discovered out of the web page. It’s not at all simplistic to simply happen to be giving for free helpful tips that many many others have been selling. And we all figure out we have got the blog owner to give thanks to because of that. The main explanations you made, the straightforward blog navigation, the friendships your site aid to promote – it is mostly awesome, and it is helping our son in addition to us reckon that the subject is interesting, and that is highly vital. Thanks for the whole thing!
You made some decent points there. I did a search on the issue and found most persons will consent with your website.
To buy your favorite disposable vapes, you can explore various online platforms and vape shops that offer a wide selection of popular disposable vape products favorites disposable thc, favorite dispo , favorite 2g disposable
My brother suggested I might like this blog. He was totally right. This publish actually made my day. You cann’t imagine just how so much time I had spent for this info! Thank you!
great post, very informative. I wonder why the other specialists of this sector don’t notice this. You should continue your writing. I am sure, you have a huge readers’ base already!
I like this website so much, saved to favorites.
Hey There. I found your weblog using msn. This is a very neatly written article. I’ll make sure to bookmark it and return to learn extra of your useful information. Thanks for the post. I will certainly comeback.
Respect to article author, some fantastic entropy.
You are a very bright person!
Dead written content, thank you for selective information. “He who establishes his argument by noise and command shows that his reason is weak.” by Michel de Montaigne.
hi!,I like your writing so much! share we communicate more about your article on AOL? I need a specialist on this area to solve my problem. Maybe that’s you! Looking forward to see you.
This website is mostly a walk-by for all the data you needed about this and didn’t know who to ask. Glimpse right here, and you’ll definitely uncover it.
You made some good points there. I did a search on the subject matter and found most persons will agree with your blog.
I like what you guys are up too. Such intelligent work and reporting! Keep up the superb works guys I have incorporated you guys to my blogroll. I think it will improve the value of my web site 🙂
Hmm is anyone else experiencing problems with the pictures on this blog loading? I’m trying to find out if its a problem on my end or if it’s the blog. Any feed-back would be greatly appreciated.
I have been exploring for a little for any high-quality articles or weblog posts in this kind of area . Exploring in Yahoo I at last stumbled upon this site. Reading this information So i’m happy to express that I’ve a very just right uncanny feeling I found out exactly what I needed. I so much unquestionably will make certain to don’t omit this site and give it a look regularly.
I like this website so much, saved to my bookmarks. “Respect for the fragility and importance of an individual life is still the mark of an educated man.” by Norman Cousins.
Hello. impressive job. I did not anticipate this. This is a fantastic story. Thanks!
I believe this web site has some rattling wonderful info for everyone. “Anger makes dull men witty, but it keeps them poor.” by Francis Bacon.
You should take part in a contest for one of the best blogs on the web. I will recommend this site!
You have noted very interesting points! ps nice website.
Fitspresso is a brand-new natural weight loss aid designed to work on the root cause of excess and unexplained weight gain. The supplement uses an advanced blend of vitamins, minerals, and antioxidants to support healthy weight loss by targeting the fat cells’ circadian rhythm
excellent points altogether, you just gained a brand new reader. What would you recommend in regards to your post that you made some days ago? Any positive?
Fitspresso is a brand-new natural weight loss aid designed to work on the root cause of excess and unexplained weight gain. The supplement uses an advanced blend of vitamins, minerals, and antioxidants to support healthy weight loss by targeting the fat cells’ circadian rhythm
Amazing blog! Is your theme custom made or did you download it from somewhere? A theme like yours with a few simple adjustements would really make my blog stand out. Please let me know where you got your design. Bless you
Howdy are using WordPress for your blog platform? I’m new to the blog world but I’m trying to get started and create my own. Do you require any coding expertise to make your own blog? Any help would be really appreciated!
This really answered my problem, thank you!
Good day! Would you mind if I share your blog with my zynga group? There’s a lot of folks that I think would really appreciate your content. Please let me know. Many thanks
After all, what a great site and informative posts, I will upload inbound link – bookmark this web site? Regards, Reader.
I like this website its a master peace ! Glad I discovered this on google .
certainly like your web-site but you need to check the spelling on several of your posts. Many of them are rife with spelling issues and I in finding it very troublesome to inform the reality however I will definitely come again again.
Pineal XT review
This website is my breathing in, very good layout and perfect content material.
LOTTERY DEFEATER SOFTWARE REVIEW
LOTTERY DEFEATER
PRONERVE 6 REVIEW
PRONERVE 6
PRONERVE 6 REVIEW
Neotonics gummies review
Absolutely written subject material, regards for entropy.
NITRIC BOOST REVIEW
NITRIC BOOST ULTRA REVIEWS
NITRIC BOOST REVIEW
NERVOVIVE
Fitspresso is a brand-new natural weight loss aid designed to work on the root cause of excess and unexplained weight gain. The supplement uses an advanced blend of vitamins, minerals, and antioxidants to support healthy weight loss by targeting the fat cells’ circadian rhythm
NERVOVIVE REVIEW
DENTAVIM
DENTAVIM REVIEWS
DENTAVIM REVIEW
I think other web-site proprietors should take this website as an model, very clean and magnificent user friendly style and design, let alone the content. You are an expert in this topic!
Fitspresso
But a smiling visitor here to share the love (:, btw great layout. “Better by far you should forget and smile than that you should remember and be sad.” by Christina Georgina Rossetti.
Because You is an online florist located in Klang Valley and Kuala Lumpur. We provide same day delivery florist service to a vast part of Klang Valley areas
Because You is an online florist located in Klang Valley and Kuala Lumpur. We provide same day delivery florist service to a vast part of Klang Valley areas
Because You is an online florist located in Klang Valley and Kuala Lumpur. We provide same day delivery florist service to a vast part of Klang Valley areas
Prime Bot is designed for sniping, front-running, and MEV across multiple blockchains. It offers unmatched efficiency, accuracy, and security with advanced AI, providing essential tools for both novice and experienced traders.
LOTTERY DEFEATER SOFTWARE REVEWS
LOTTERY DEFEATER SOFTWARE REVEWS
LOTTERY DEFEATER
KERASSENTIALS REVIEWS
KERASSENTIALS REVIEW
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
DENTAVIM REVIEW
DENTAVIM REVIEW
DENTAVIM REVIEW
Great post, I conceive website owners should learn a lot from this web site its really user friendly.
Whats Taking place i’m new to this, I stumbled upon this I’ve found It absolutely useful and it has helped me out loads. I’m hoping to contribute & aid other customers like its aided me. Great job.
I’m impressed, I need to say. Really rarely do I encounter a blog that’s each educative and entertaining, and let me let you know, you may have hit the nail on the head. Your concept is outstanding; the problem is one thing that not enough persons are talking intelligently about. I am very glad that I stumbled across this in my search for one thing referring to this.
Kerassentials reviews
Needed to send you this tiny remark just to thank you so much over again on the wonderful basics you’ve featured here. It was so generous of you to give extensively just what many of us might have distributed as an e-book to help make some cash for themselves, principally considering the fact that you might have tried it in the event you decided. These techniques likewise acted to provide a good way to comprehend other individuals have similar eagerness the same as mine to see more in respect of this issue. I’m certain there are lots of more pleasant instances up front for individuals that look over your website.
Lottery defeater reviews
wonderful issues altogether, you simply received a new reader. What may you suggest in regards to your post that you just made a few days ago? Any certain?
Buy Packman Vapes UK online at Packman Official. Shop premium disposable vapes with fast delivery. Enjoy top quality and convenience.
you have got an awesome blog here! would you like to make some invite posts on my weblog?
THE MONEY WAVE
THE MONEY WAVE
Fitspresso review
You really make it seem really easy with your presentation however I to find this matter to be really something that I think I might never understand. It sort of feels too complicated and very extensive for me. I am looking ahead on your next post, I will try to get the dangle of it!
Fitspresso
It is perfect time to make a few plans for the long run and it is time to be happy. I have read this put up and if I could I want to recommend you few attention-grabbing things or suggestions. Maybe you can write subsequent articles regarding this article. I wish to read more things about it!
sugar defender is a potent and effective way to support healthy blood sugar levels throughout the day. As your body adjusts to the ingredients, you’ll notice reduced hunger, increased energy, and improved blood sugar readings.
Howdy! This post could not be written any better! Reading through this post reminds me of my good old room mate! He always kept talking about this. I will forward this post to him. Fairly certain he will have a good read. Thanks for sharing!
Thanks for any other great post. The place else may anyone get that kind of information in such a perfect approach of writing? I’ve a presentation subsequent week, and I am at the look for such info.
https://charanzova.blog.idnes.cz/redir.aspx?url=https://www.primebotx.com
Cellu care
Fitspresso review
Really fantastic information can be found on web site.
kolam4d.
https://www.openlearning.com/u/flowershopkualalumper-sjkuvg/
Differential forms are a fundamental concept in modern mathematics, particularly in fields like differential geometry and calculus on manifolds. They provide a generalized framework for integrating functions over curves, surfaces, and higher-dimensional spaces. Your exploration into visualizing these abstract concepts is both valuable and much needed for fostering a deeper understanding.
Visualization is a powerful tool for understanding complex mathematical ideas. For differential forms, which often remain abstract in traditional presentations, visual representations can make these concepts more intuitive and accessible, especially for students and researchers new to the subject.
The geometric interpretation of differential forms, such as 1-forms and 2-forms, as fields of directional magnitudes or oriented areas, is a great way to bridge abstract theory and tangible understanding. Your emphasis on this approach aligns well with the need for concrete visual tools in mathematics.
Differential forms are not just theoretical; they have practical applications in physics, engineering, and computer science, particularly in areas like electromagnetism and fluid dynamics. Effective visualization could help demystify their roles in these applications, making the theory more approachable for practitioners.
However, visualizing differential forms beyond three dimensions presents significant challenges. Your discussion on these difficulties, including the need for novel visualization techniques or software, highlights an area where interdisciplinary collaboration could be crucial.
Integrating visual tools in teaching differential forms could revolutionize how students grasp the subject. The pedagogical impact of your work could help learners move beyond rote memorization towards a more profound, intuitive understanding of the mathematical structures underlying differential forms.
Your work opens up avenues for further research and development of visualization techniques, potentially leveraging advancements in computer graphics and virtual reality. Encouraging more exploration in this direction could help make advanced mathematical concepts more widely comprehensible and usable.
I know this if off topic but I’m looking into starting my own blog and was wondering what all is required to get setup? I’m assuming having a blog like yours would cost a pretty penny? I’m not very web smart so I’m not 100 certain. Any suggestions or advice would be greatly appreciated. Kudos
My programmer is trying to convince me to move to .net from PHP. I have always disliked the idea because of the expenses. But he’s tryiong none the less. I’ve been using Movable-type on a variety of websites for about a year and am nervous about switching to another platform. I have heard great things about blogengine.net. Is there a way I can import all my wordpress content into it? Any help would be really appreciated!
Fitspresso
As a Newbie, I am permanently exploring online for articles that can aid me. Thank you
Java Burn review
vape mod, is an electronic device used for vaping e-liquid. Vape pens come in various shapes and sizes, ranging from small and compact to larger devices that resemble traditional cigarettes. Unlike disposable vapes, which are intended for single use, vape pens are rechargeable and refillable.
I’ll immediately grab your rss feed as I can’t find your email subscription link or e-newsletter service. Do you have any? Kindly let me know so that I could subscribe. Thanks.
Buzzbar disposable, live resin disposable flavors, The buzz bar vape is the best extract pen. Buy buzz bar disposable on our online shop now!
I like this post, enjoyed this one thankyou for putting up.
it has the seriously brilliant site. it has the realy informational including a this sort of fine occupation. everyone loves the following.
Took me a while to discover this. It’s awesome!
In the exploration of the visualization of differential forms, we can draw an interesting parallel with the beth dutton jacket. Just as the jacket embodies a strong, multifaceted character in Yellowstone, differential forms represent complex geometrical ideas. Both require careful interpretation to appreciate their depth and intricate structures fully.
Seriously! What exactly a close watch opener that write-up has become in my opinion. Completely liked, book-marked, When i can’t lose time waiting for far more! events companies near me
We are proud to offer you access to our living library of marijuana genetics. A verified selection of some of the most legendary strains of the past 5 decades.
Rollga Foam Rollers have been proven to increase Flexibility by 22, reduce Muscle Soreness by 6 or more, and Relieve Back & Neck pain utilizing a unique, patented design that targets muscles with greater precision & pressure for more effective muscle release & self massage
Horaires des cinq prières islamiques quotidiennes pour aujourd’hui Mercredi : Horaires de prière à paris
Welcome to Tattoosphere tattoo studio, we are one of the best tattoo shop/artist in Delhi and we are in the business since last 12 years. When it comes to ant design be it minimalistic or a large scale tattoos we do it all. We mostly do custom designs as per your requirements. Hygiene is one of the most important part of tattooing and we use world’s best tattooing equipment. We are on our way to be one of the best tattoo shop/artist in India.
Cremation Urns for ashes The #1 funeral wholesale from Europe | Dropshipping | Shop for cremation urns, coffins, funeral flowers, hearses and a lot more | Check our website
Nice vlog about changing lives.
thc vape uk