A compressed full-text self-index for a text
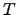
, of size
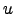
, is a
data structure used to search patterns
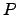
, of size
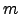
, in
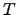
that
requires reduced space, i.e. that depends on the empirical entropy
(
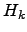
,
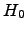
) of
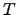
, and is, furthermore, able to reproduce any
substring of
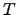
. In this paper we present a new compressed self-index
able to locate the occurrences of
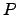
in
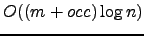
time, where
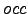
is the number of occurrences and
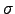
the size
of the alphabet of
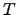
. The fundamental improvement over previous LZ78
based indexes is the reduction of the search time dependency on
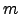
from
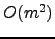
to
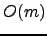
. To achieve this result we point out the main
obstacle to linear time algorithms based on LZ78 data compression and
expose and explore the nature of a recurrent structure in LZ-indexes,
the
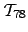
suffix tree. We show that our method is very
competitive in practice by comparing it against the LZ-Index, the
FM-index and a compressed suffix array.