Flow
around a NACA 0012 airfoil
1.
Domain
size
The domain for the calculation of the flow
over around the NACA 0012 airfoils is a rectangle of length ![]() and width
and width
![]() , where
, where ![]() is the chord of the airfoil.
The inlet is located
is the chord of the airfoil.
The inlet is located ![]() upstream of the
leading edge of the airfoil and the outlet is placed
upstream of the
leading edge of the airfoil and the outlet is placed ![]() downstream of the
trailing edge of the airfoil. The external boundary is located approximately
downstream of the
trailing edge of the airfoil. The external boundary is located approximately ![]() away from the airfoil.
The Reynolds number based on the velocity of the incoming flow
away from the airfoil.
The Reynolds number based on the velocity of the incoming flow
![]() , chord of the foil
, chord of the foil ![]() and kinematic
viscosity
and kinematic
viscosity ![]() is
is ![]() .
.
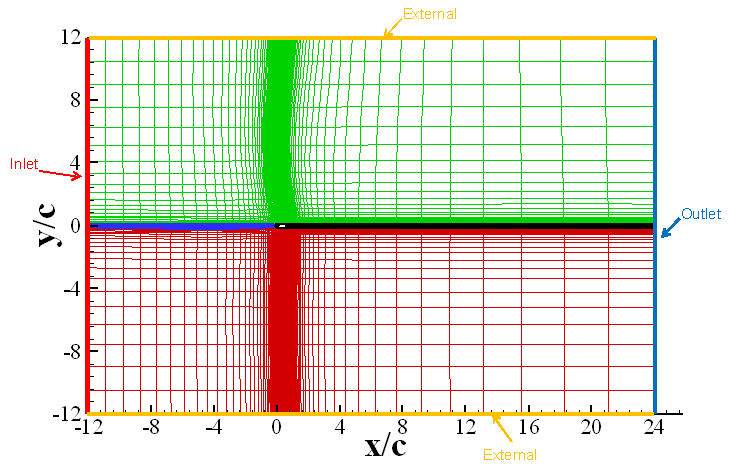
The Cartesian coordinate system has the
horizontal component ![]() aligned with the
incoming flow and the trailing edge is located at
aligned with the
incoming flow and the trailing edge is located at ![]() . The chord
. The chord ![]() makes an angle
makes an angle ![]() with the
with the ![]() axis, defining the
angle of attack.
axis, defining the
angle of attack.
2.
Boundary
Conditions
· Inlet
Horizontal
velocity component equal to incoming velocity (![]() ) and vertical
velocity component equal to zero (
) and vertical
velocity component equal to zero (![]() ).
).
Pressure extrapolated
from the interior of the domain.
Turbulence kinetic
energy equal to ![]() , turbulence frequency equal to
, turbulence frequency equal to 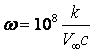 and undamped
eddy-viscosity equal to
and undamped
eddy-viscosity equal to ![]() .
These inlet turbulence quantities lead to
.
These inlet turbulence quantities lead to 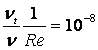 for the two-equation
models and
for the two-equation
models and 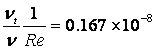 for the Spalart & Allmaras
one-equation model.
for the Spalart & Allmaras
one-equation model.
· Outlet
Derivatives of
horizontal and vertical velocity components in the horizontal direction equal
to zero (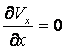 ,
, 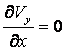 ).
).
Derivative
of pressure in the horizontal direction equal to zero (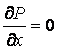 ).
).
Derivatives of
turbulence kinetic energy, turbulence frequency and undamped
eddy-viscosity in the horizontal direction equal to zero (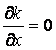 ,
, 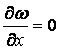 ,
,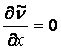 ).
).
· External
Derivatives
of horizontal velocity component in the vertical direction equal to zero (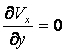 ) and vertical
velocity components equal to zero (
) and vertical
velocity components equal to zero (![]() ).
).
Pressure
derivative in the vertical direction equal to zero (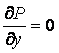 ).
).
Derivatives of
turbulence kinetic energy, turbulence frequency and undamped
eddy-viscosity in the vertical direction equal to zero (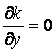 ,
, 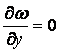 ,
, 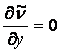 ).
).
· Airfoil surface
Horizontal and vertical
velocity components equal to zero (![]() ,
, ![]() ).
).
Pressure
derivative in the vertical direction equal to zero (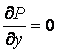 ).
).
Turbulence kinetic
energy and undamped eddy-viscosity equal to zero (![]() ,
, ![]() ) and
turbulence frequency specified at the near-wall cell centre (
) and
turbulence frequency specified at the near-wall cell centre (![]() ) from the
analytical solution of the
) from the
analytical solution of the ![]() transport equation (
transport equation (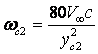 ).
).![]() is the distance of the near-wall cell centre to the surface
of the foil.
is the distance of the near-wall cell centre to the surface
of the foil.
Pressure is set equal to zero at the top left corner of
the Inlet to specify the pressure level (all
pressure boundary conditions are related to pressure derivatives).
3.
Grids
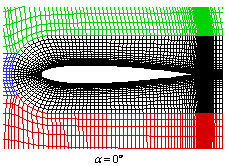
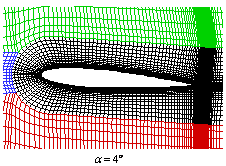
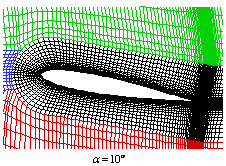
For each of the angles of attack there are 6
sets of 9 geometrically similar grids available (typical grids are illustrated
at the top of this page). The number of cells of the grids is the same for all
the sets that differ only on the distribution of grid nodes along the vertical
direction of the black, red and green blocks and horizontal direction of the blue block. Set 1 contains the smallest vertical height
of the near-wall cells and the largest expansion ratio, whereas set 6 includes
the largest vertical height of the near-wall cells and the smallest expansion
ratio. Distribution of grid nodes in the vertical direction of black, red and green
blocks and horizontal direction of the blue
block is defined by one-sided stretching functions proposed by Vinokur.
For the sake of completeness, the largest,
average and smallest dimensionless distance of the near-wall cell centre to the
airfoil surface ( ) are included in the file that contains the lift (
) are included in the file that contains the lift (![]() ) and drag (
) and drag (![]() ) coefficients
of the airfoil.
) coefficients
of the airfoil. ![]() is the friction velocity defined by
is the friction velocity defined by 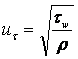 where
where ![]() is the shear-stress at
the wall and
is the shear-stress at
the wall and ![]() is the fluid density.
is the fluid density.
The grid refinement ratio ri
may be obtained from the total number of cells Ncells
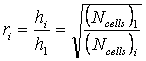
The number of cells is independent of the
angle of attack ![]() and the values of Ncells and ri are given below.
and the values of Ncells and ri are given below.
|
ri |
Ncells |
|
CASES IV, V and VI |
|
|
1.000 |
929280 |
|
1.143 |
711480 |
|
1.333 |
522720 |
|
1.600 |
363000 |
|
2.000 |
232320 |
|
2.286 |
177870 |
|
2.667 |
130680 |
|
3.200 |
90750 |
|
4.000 |
58080 |